编译原理学习笔记

Posted by Mr.Be1ieVe on Saturday, June 27, 2020

视频

编译器结构

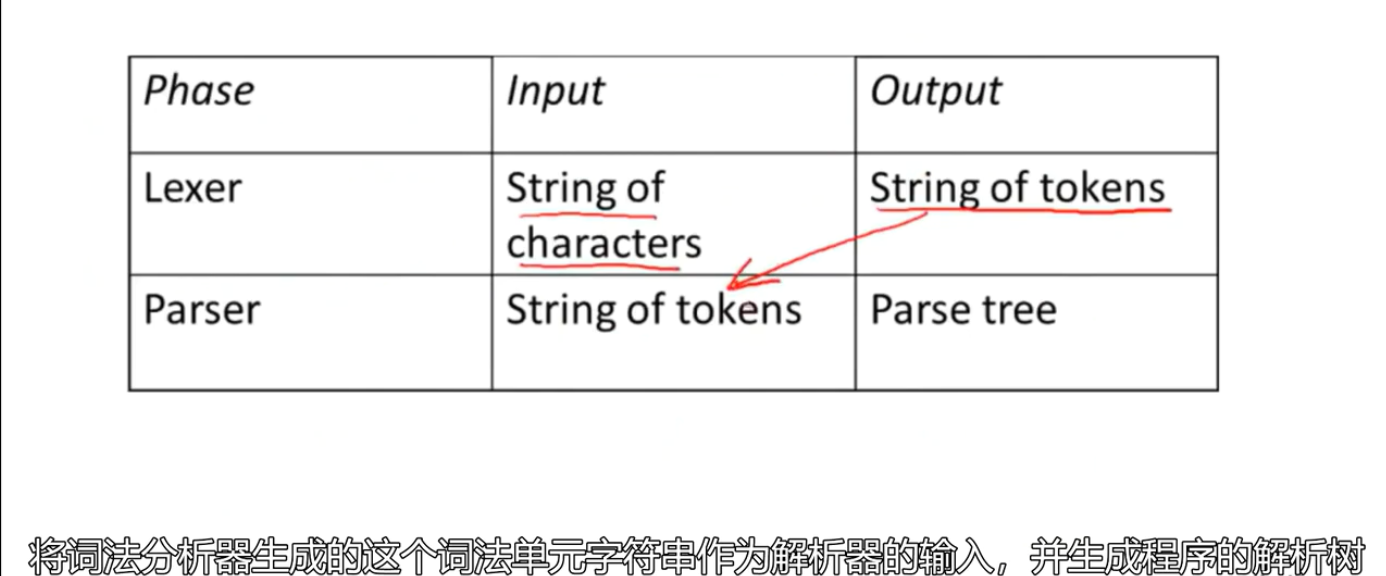
词法分析 Lexical analysis or scanning

检测输入字符串中不属于我们语言的那部分符号

词法分析把程序字段变成关键字words or 词法单元tokens

如

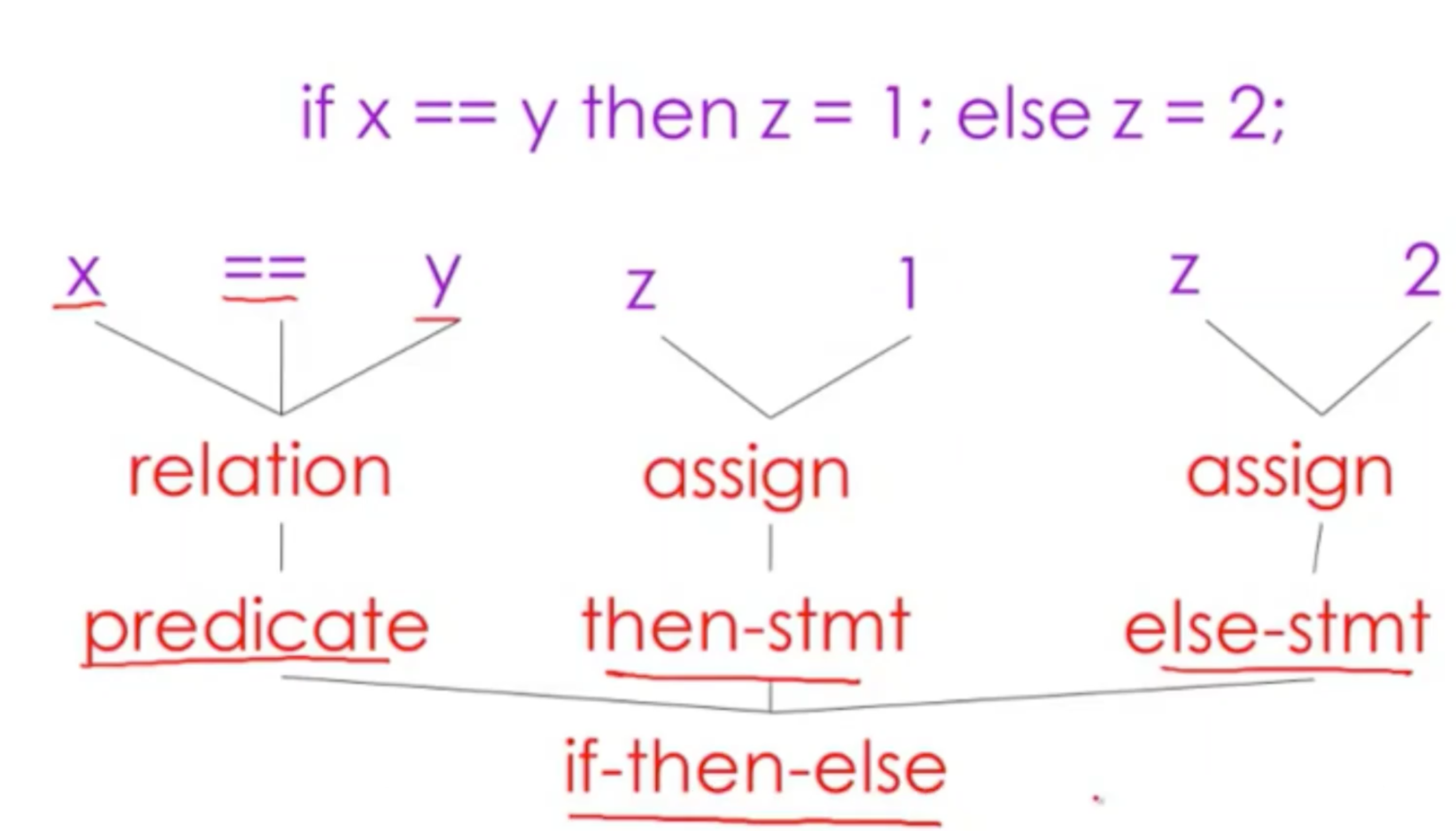
if x == y then z = 1; else z = 2;

分号，标点，分隔符都是词法单元

语法分析syntax analysis parsing

试着去判断是否格式正确或者是否是有效程序（语句中是否存在格式错误或没用解析树）

if then else包含三部分

predicate条件判断，then语句和else语句

image-20200626235143347

语义分析 semantic analysis

尝试去找出矛盾的地方

优化 optimization

修改代码使之使用更少的资源

代码生成

高级语言转变成汇编

Cool语言

class Main {
 i : IO <- new IO;
 main() : Int { { i.out_string("Hello wordld!\n"); 1;} };
};

Int 是return type。

class Main {
 i : IO <- new IO;
 main() : IO { { i.out_string("Hello wordld!\n"); } };
};//一旦打印完string就退出

class Main {
 i : IO <- new IO;
 main() : Object { { i.out_string("Hello wordld!\n"); } };
};//Object 返回类型

class Main {
 main() : Object { { (new IO).out_string("Hello wordld!\n"); } };
};

下面是继承的写法

class Main inherits IO{
 main() : Object { { self.out_string("Hello wordld!\n"); } };
};

class Main inherits IO{
 main() : Object { { out_string("Hello wordld!\n"); } };
};

词法分析

目标是将输入流划分为词素。

从左到右的扫描字符串，有时必须对输入字符串向前看，才能弄清楚当前字符串和子字符串在语言中的角色

变量名称：字母开头

字符串-> 语法分析器 ->变成token<class, string> parser解析器

foo = 42 -> <Id, “foo”> <operator, “="> <Int, “42”>

有以下几类：

  • 空格whitespace
  • keyword
  • identifiers
  • numbers

这些子字符串称为词素（构成词的要素），<token class， lexemes词素>，这就是一个token

正则表达式

基础表达式

单字符

‘c’ = {‘c’}

Epsilon

Epsilon = {”"} = 单个字符的空字符串 != 空字符串

复合表达式

Union

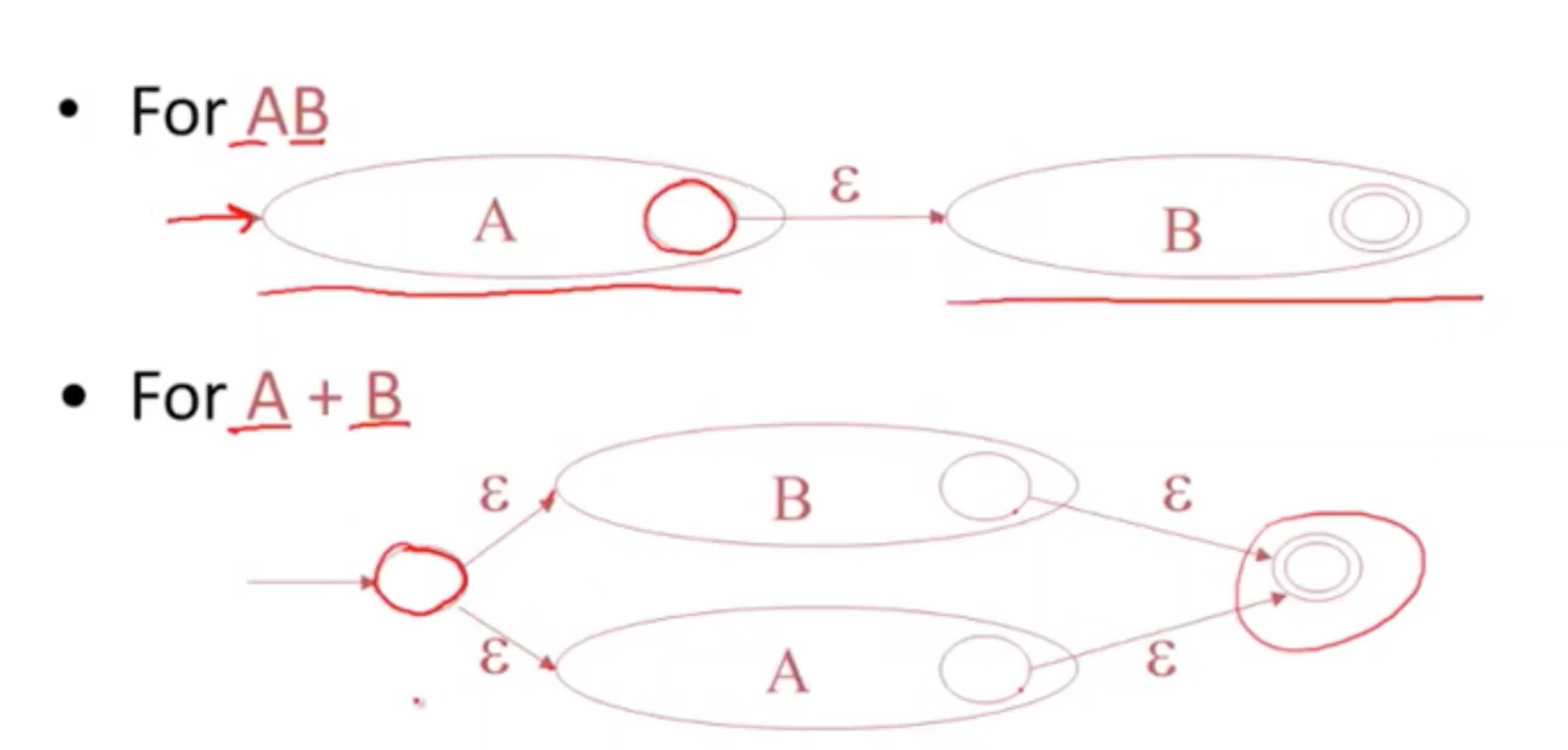
A + B = {a|a属于A} U {b|b属于B}

A并B

Concatencation 级联

如[a,b]与[c,d]级联得到[ac,ad,bc,bd]

AB = {ab | a属于A ^ b 属于B }

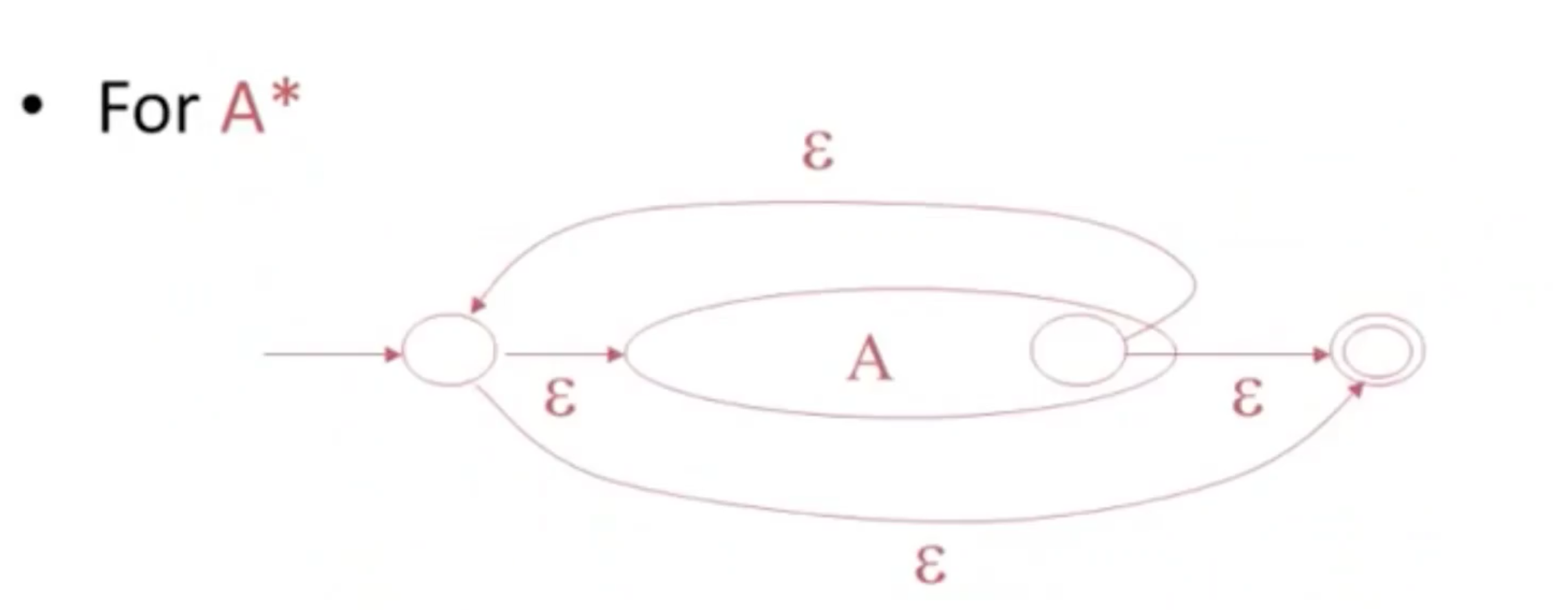
Iterator 串联

A* = 0到无穷个A串联

匹配变量名

A+ = AA* = 至少一个A

digit = ‘0’ + ‘1’ + ‘2’ + ‘3’ + ‘4’ + ‘5’ + ‘6’ + ‘7’ + ‘8’ + ‘9’

letter = [a-zA-Z] 匹配所有字母

letter(letter+digit)* 字母+0或多个字母和数字的组合

空格 ’ ’ + ‘\n’ + ‘\t’

opt_function = (’.‘digits)?

Opt_exponent = (‘E’(’+’ + ‘-’)?digits)?

###词法规范

当输入值有两种不同的前缀，且这两种都是有效的词法单元时，就应该选择最长的那个，最长匹配原则Maximal Munch

当匹配到两个规则的时候，如keiword，identifiers，会优先匹配第一个choose the one listed first。

捕获有可能错误字符串的正则表达式并赋予其最低优先级

有限自动机Finite Automata

定义

  • 一组能读取的输入字符串
  • 一个有限状态的集合
  • 一个特殊的集合被设定为开始状态
  • 一组用于接受状态的集合（读取完可接受状态输入后自动结束，否则拒绝输入
  • 有一些用于状态转换的集合

image-20200628214134850

Exampls

image-20200628160825195

确定性自动机和非确定性自动机的区别

image-20200628161433100

DFA只有一条道可以通过

NFA基于输入执行，可能处于许多不同的状态，只要有任何一条路径可以接受，就会处于接受状态 ，这个字符串就属于这个NFA可以接受的语言

image-20200628161945645

NFA要远比DFA来的小，可以成倍缩小，DFA执行速度更快

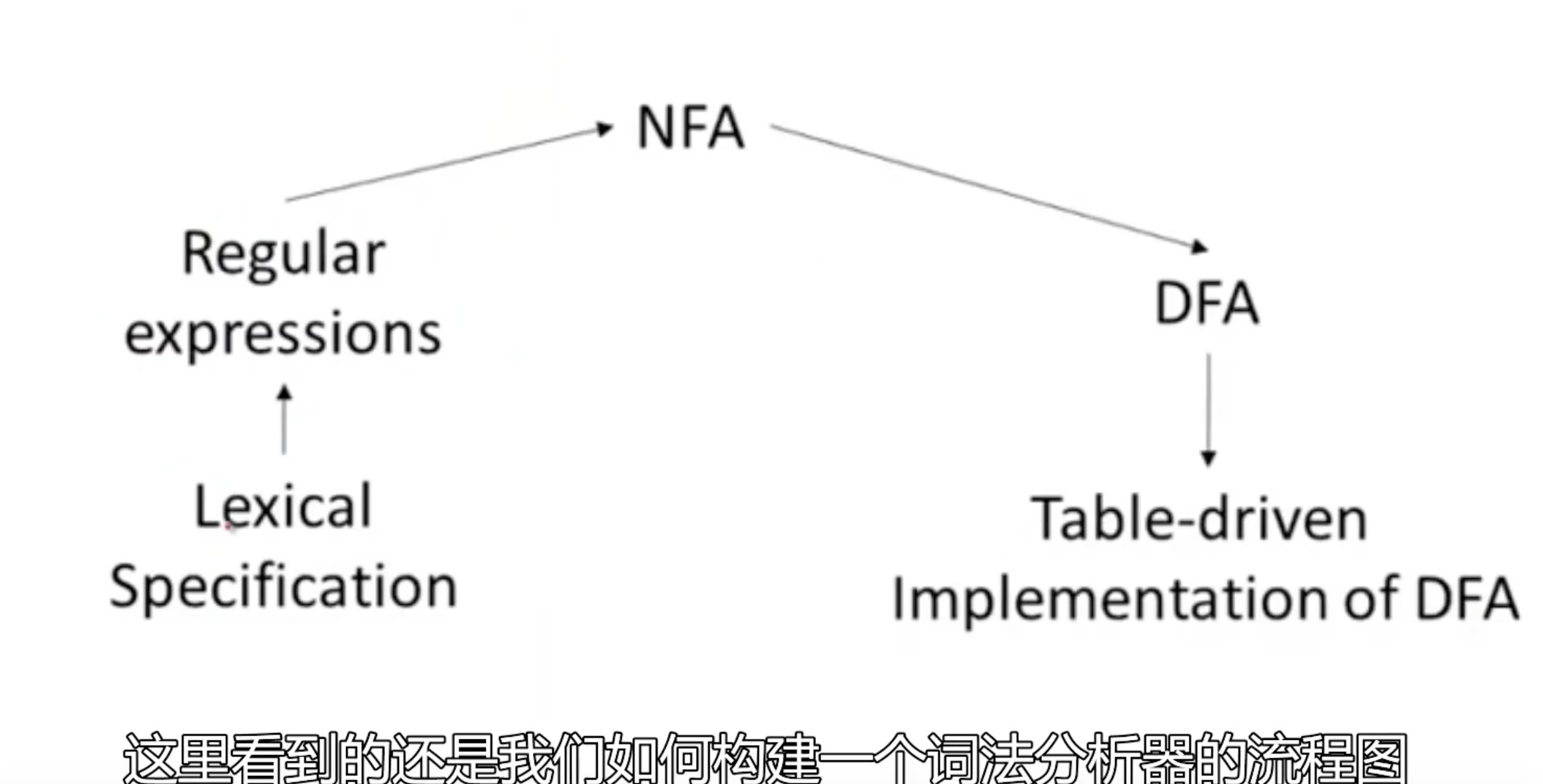
将正则表达式转换为NFA 非确定性有限自动机

image-20200628213856496

image-20200628213913515

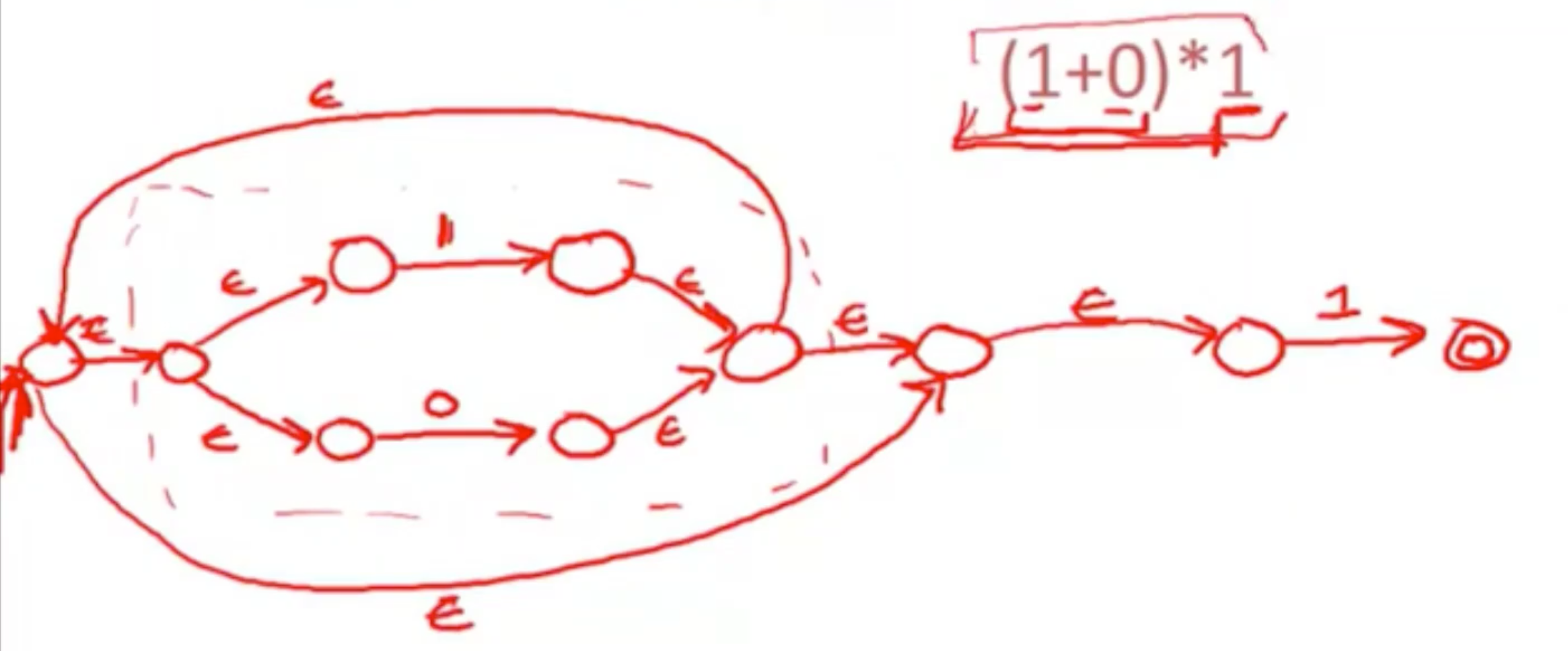
image-20200628213950201

NFA to DFA

Epsilon-closure：是状态选择，可以是一组状态，但只针对单个状态进行处理，只关注那些仅通过空跳就可以到达的状态。

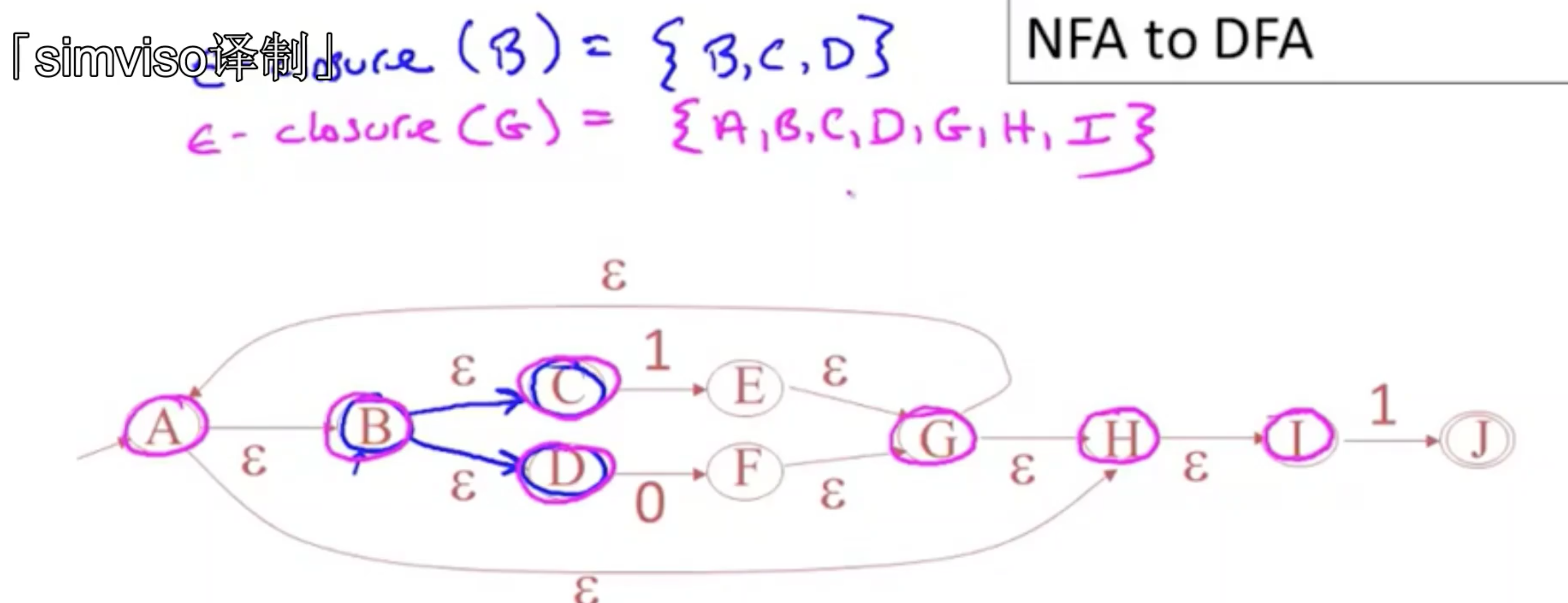
image-20200628215245905

N种状态，可用状态数量子集|S| <= N，公用2^N -1种非空子集

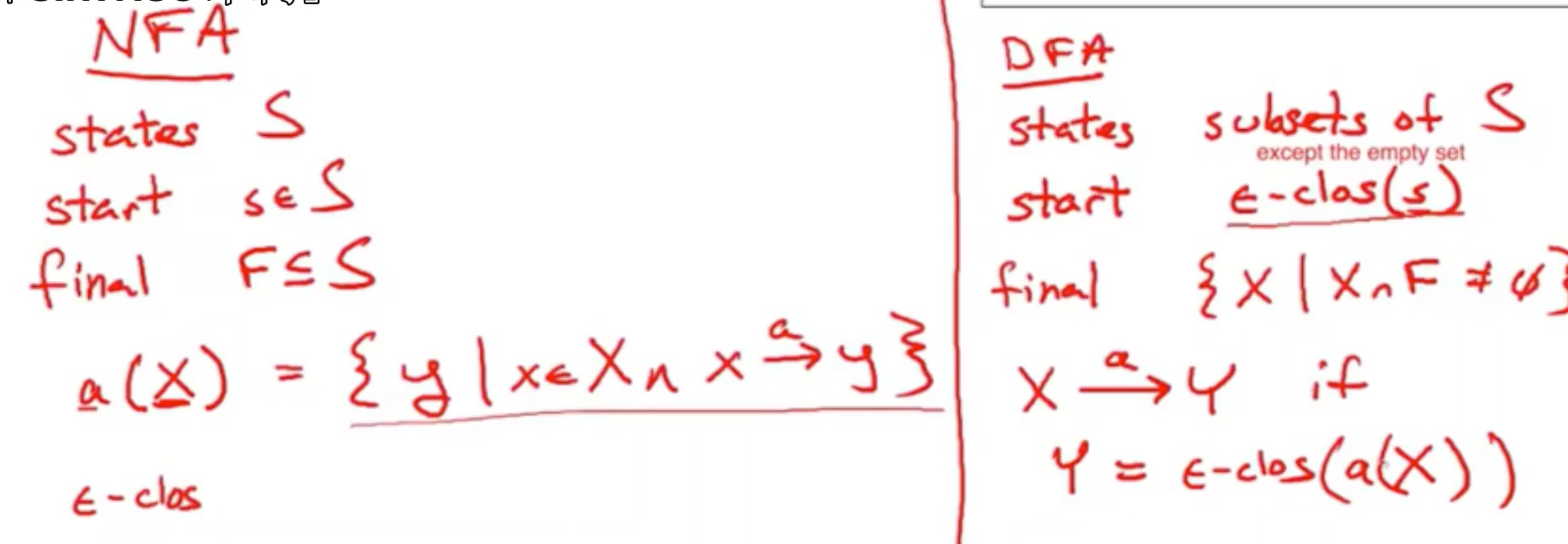
image-20200628220546136

所维护的每一个属性都指代一条计算执行路径，DFA的状态记录了NFA基于相同输入可能进入的可能状态集

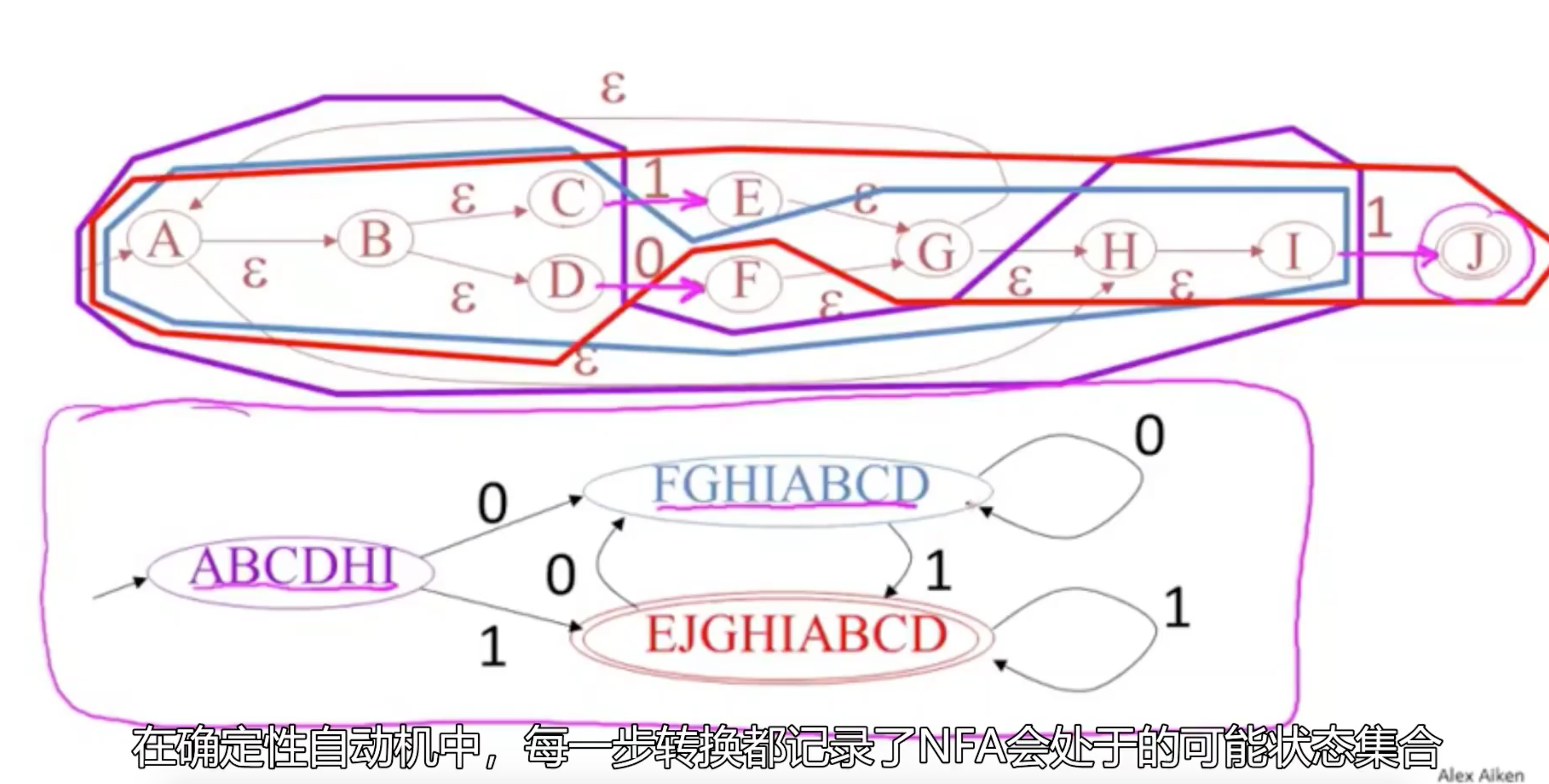
image-20200628221202160

原视频讲解链接：link 11:15秒

实现有限自动机

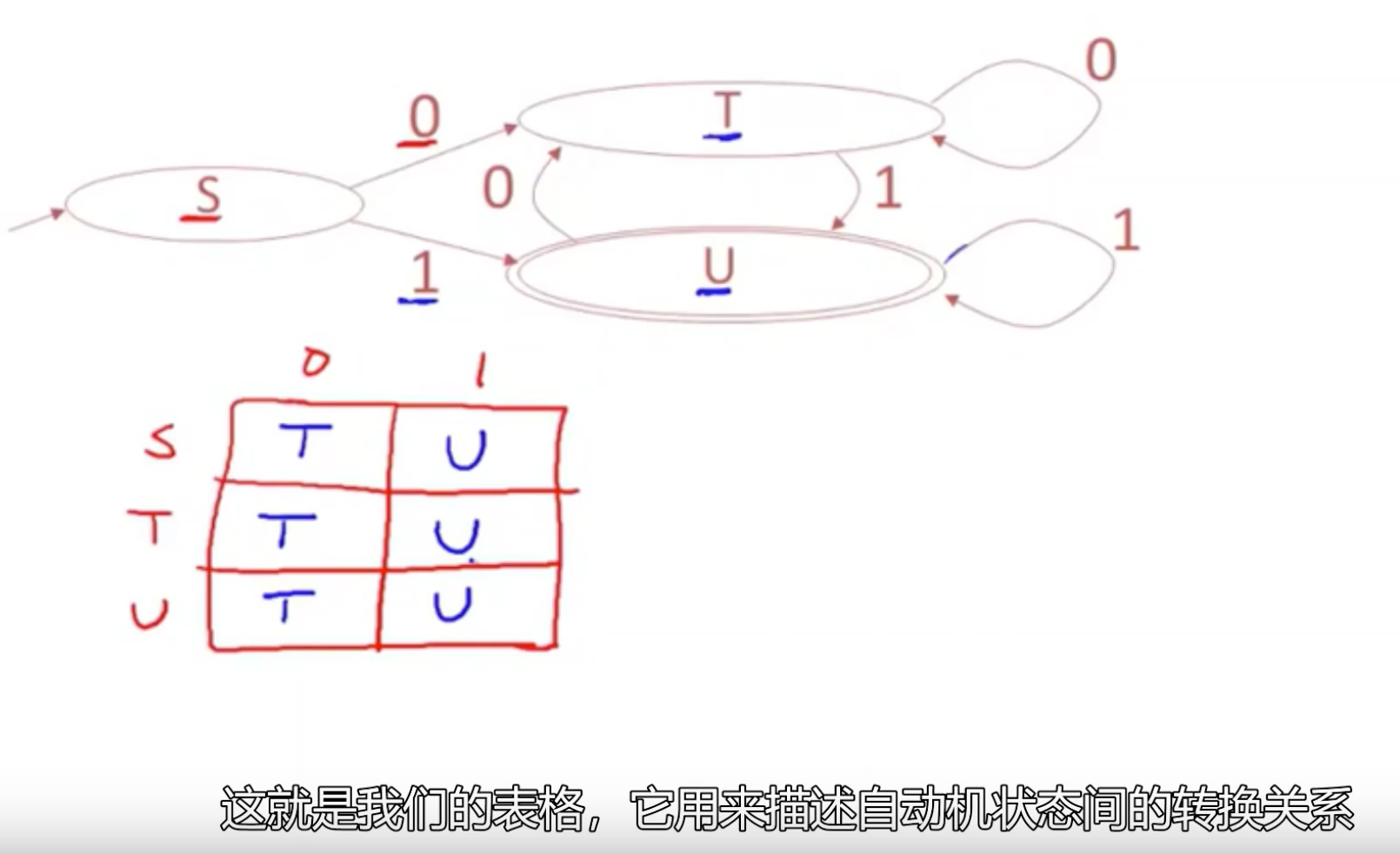
image-20200628221706335

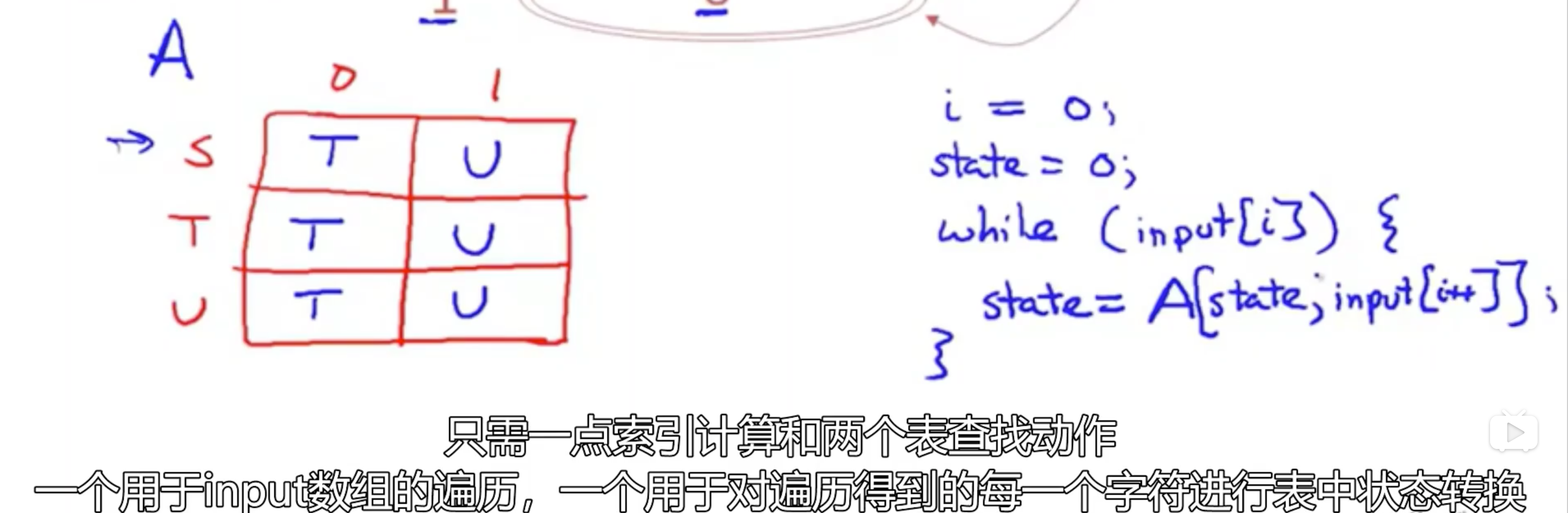
image-20200628222154758

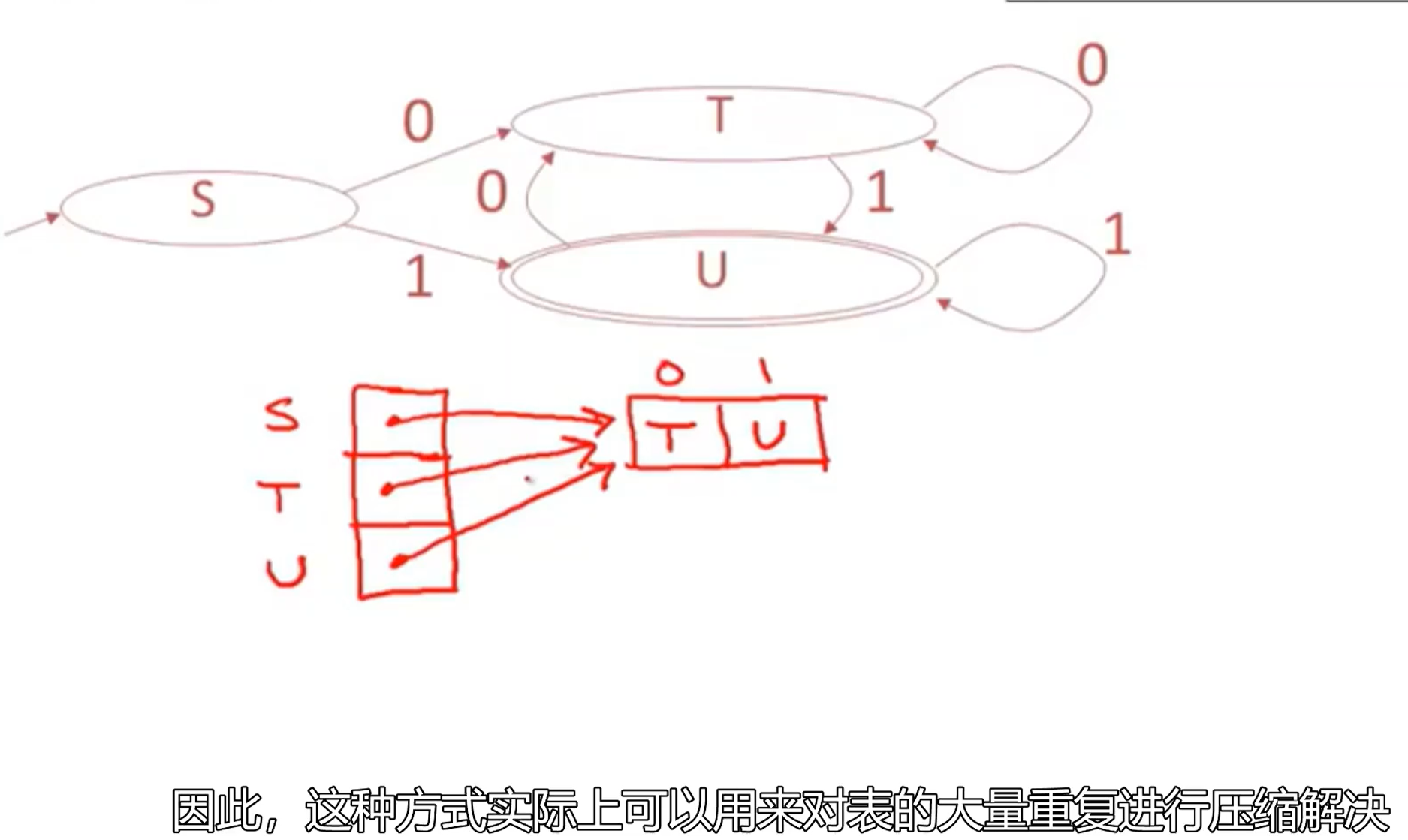
image-20200629082652419

实现NFA

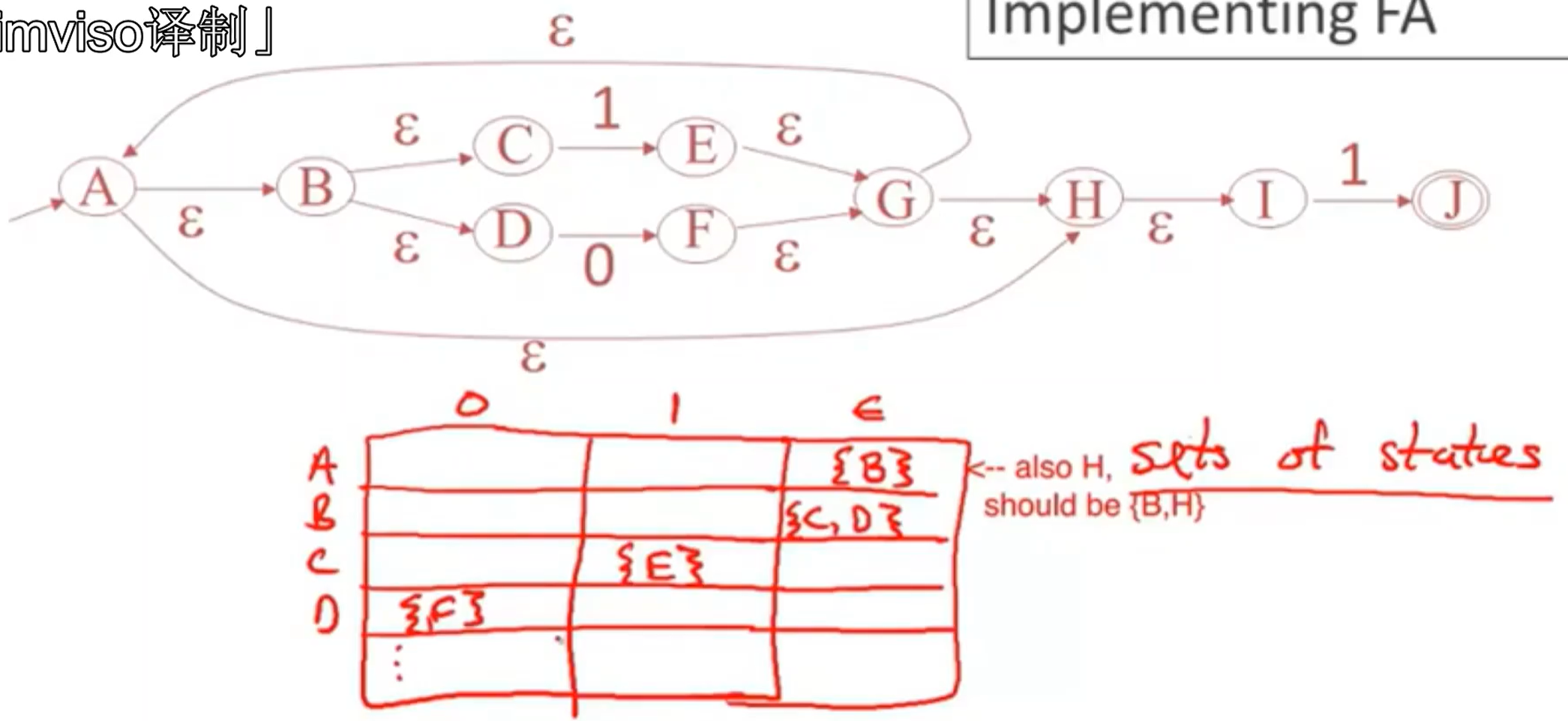
image-20200629083217424

节省了大量表空间，但是

执行速度比确定性自动机慢很多

总结

DFA执行速度更快，结构上较为松散

NFA速度较慢，结构紧凑

PA2

https://github.com/mrbelieve128/Stanford-Compilers-PA/tree/master/PA2

解析器 Parsing

image-20200707171225807

上下文无关文法 context-free grammar

  • 不是所有token都是程序
  • 解析器parse需要分辨有效和无效的字符串

所以需要

  • 需要中算法来分辨有效token
  • 算法来分辨有效token和无效token

上下文无关的文法自然而然地用于描述这种递归结构

image-20200708102409480

上下文无关的文法包含

  • A set of terminals T
  • A set of non-terminal N
  • A start symbol S (S 是 N之一)
  • A set of productions (是指一个符号跟着一个箭头，紧接着一串符号)

image-20200708103010382

定义7:43左右

推导

Example

Grammer

E -> E+E | E*E | (E) | id

String

id * id + id

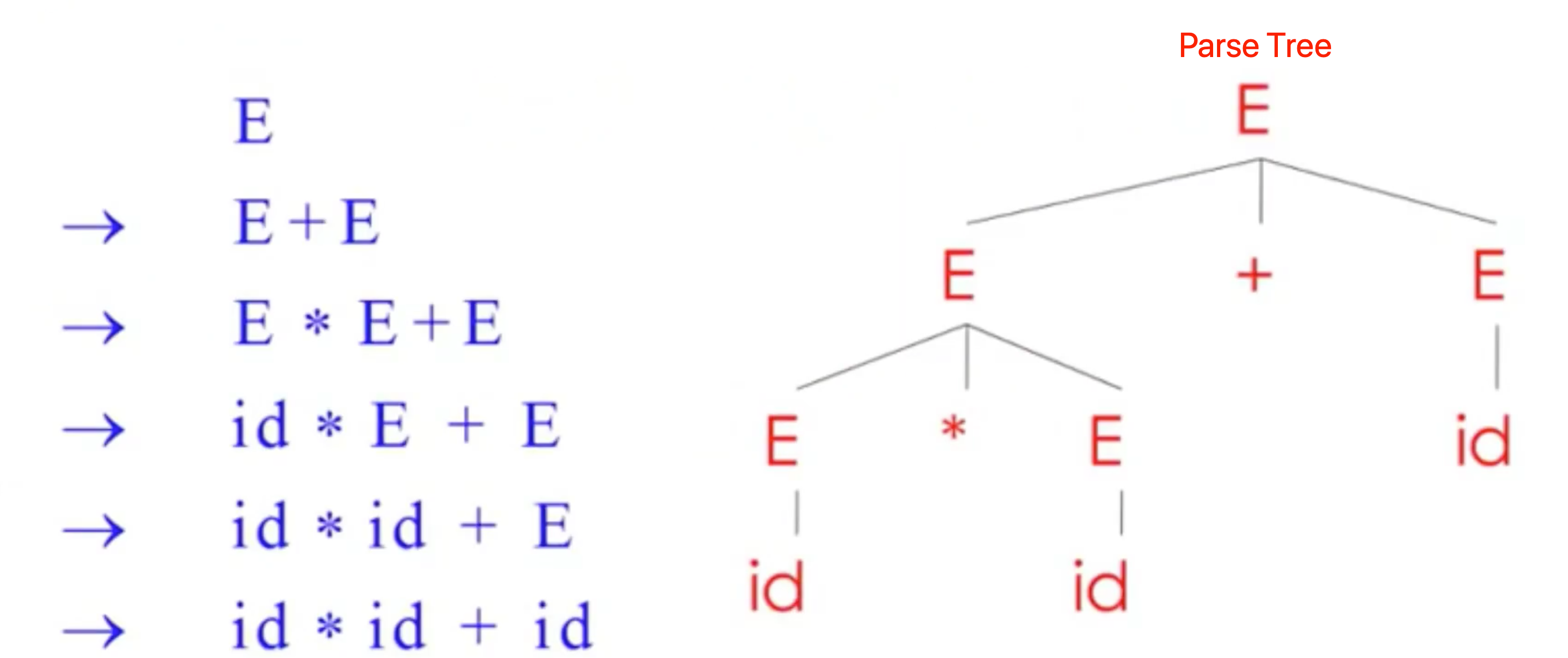
image-20200708111200187

A parse tree has

  • Terminals at the leaves
  • Non-terminals at the interior nodes (内部节点)

叶子结点的中序遍历结果是原始输入

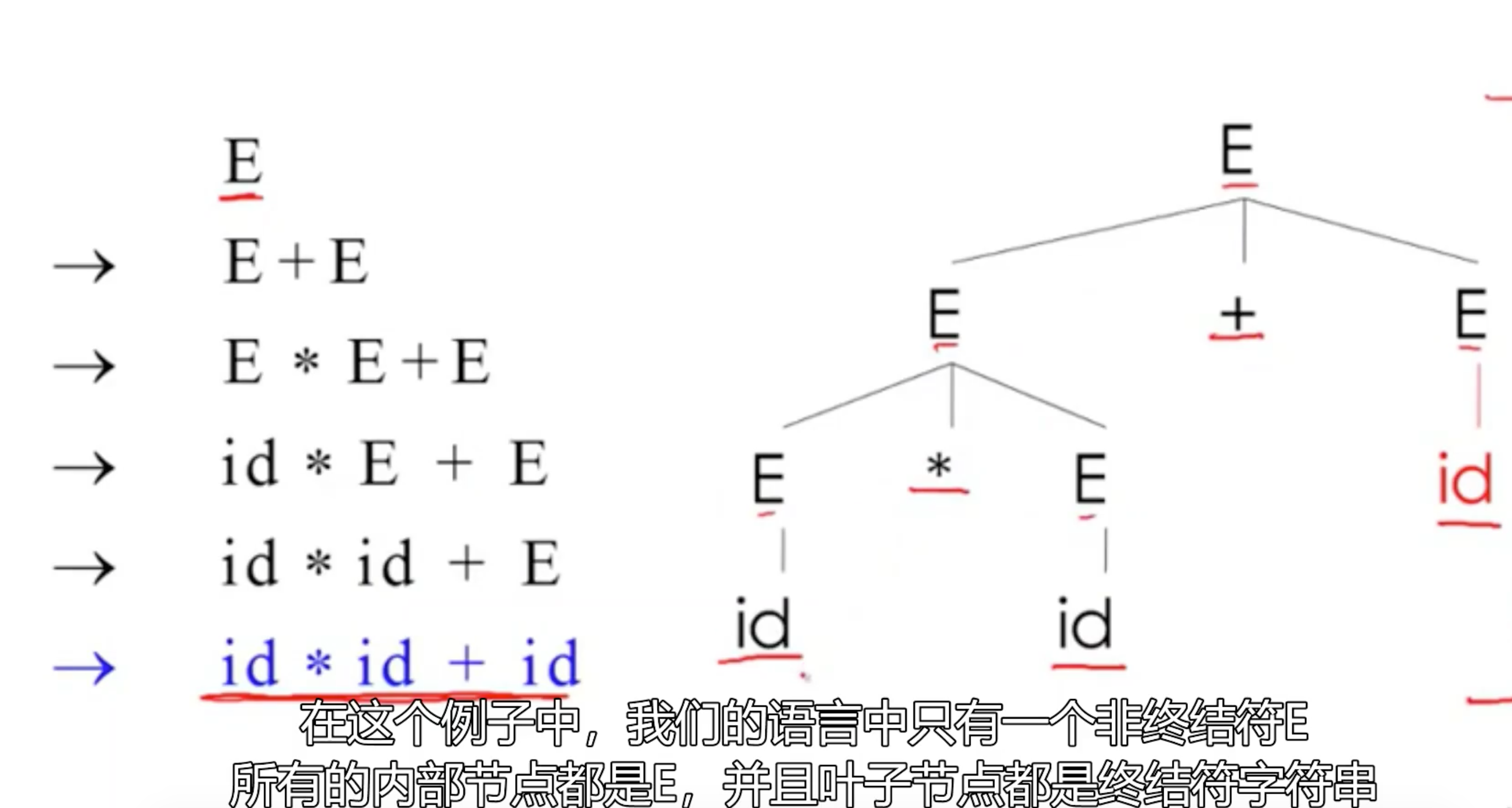
image-20200708111904374

解析树也展示了操作间的关联性，但输入字符串并没有展示

如上图，**""要比"+"**号更优先，因为号是+号的子树

上图这个例子是最左推导(在每个步骤先替换最左边的非终结字符）也有个等价概念最右推导

最左和最右推导生成的解析树都是一样的

总结

image-20200708113045442

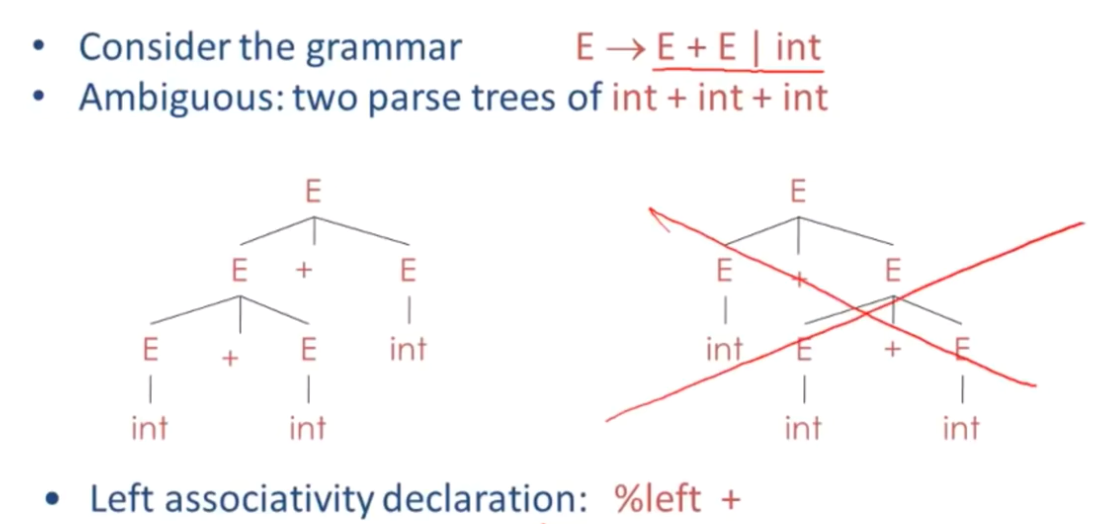
Ambiguity 歧义性

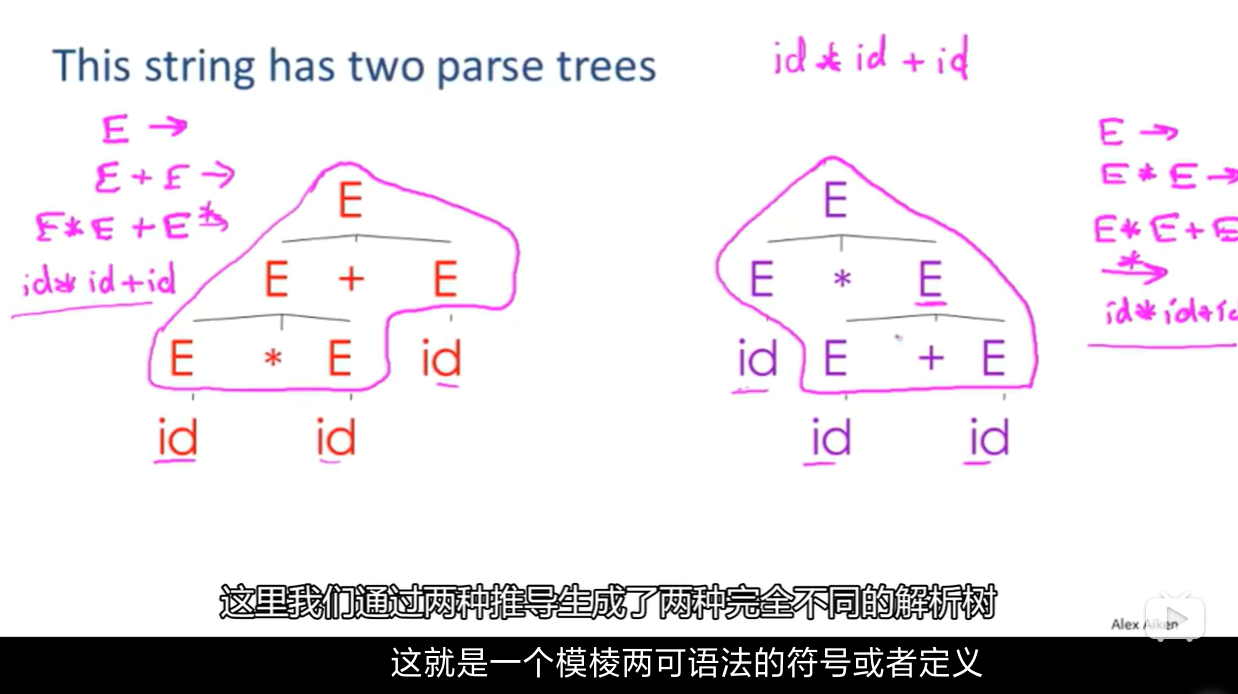
  • 如果对于某个字符串有多个解析树，那么这个语法就是模棱两可的。或者说，对于某个字符串有多个最右推导或者最左推导，那么这个字符串就会有两个截然不同的解析树，语法也会变得有歧义
  • Ambiguity is BAD

消除歧义性得最直接办法是重写语法，生成相同语法但生成单一解析树

E -> E’ + E | E’

E’ -> id * E’ | id | (E) * E’ | (E)

image-20200708151619295

if-then-else结构

image-20200708152324929

总结

  • Impossible to convert automatically an ambiguous grammar to an unambiguous one

  • User with care, ambiguity can simplify the grammar

    sometimes allows more natural definitions

    We need disambiguation mechanisms

  • Instead of rewriting the grammar

    Use the more natural (ambiguous) grammar

    Along with disambiguating declarations

  • Most tools allow precedence and associativity declarations(优先性和关联性声明) to disambiguate grammars

image-20200708153308814

image-20200708153242579

错误处理

image-20200708211223360

紧急模式

最简单，最广泛使用的

检测到错误，解析器会开始抛弃 token直到找到作用明确的token

image-20200708211933630

错误产生式

将常犯的已知错误指定为语法中的替代产生式

image-20200708214135600

自动局部或全局校正

image-20200708214329681

抽象语法树 Abstract Syntax Trees

  • Like parse trees but ignore some details
  • Abbreviated as AST （简称AST）

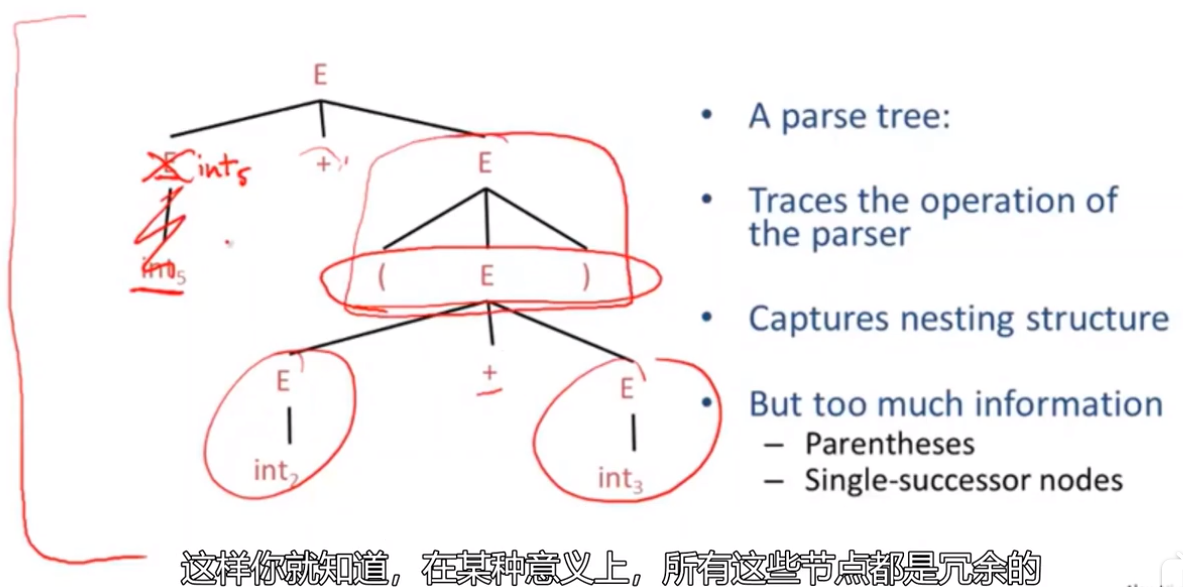
image-20200708215810670

下图表示了上图相同的内容

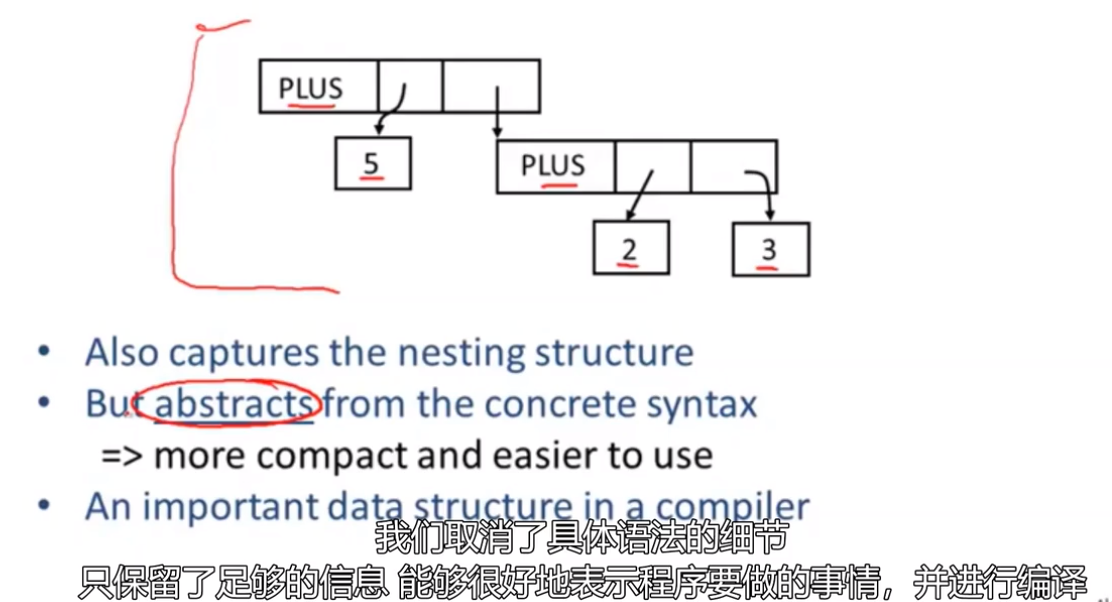
image-20200708215745811

递归下降解析

image-20200709092646974

image-20200709093014117

将E变成与(int)相同的格式使之可以匹配，则算解析成功，所以E->T->(E)->(int)

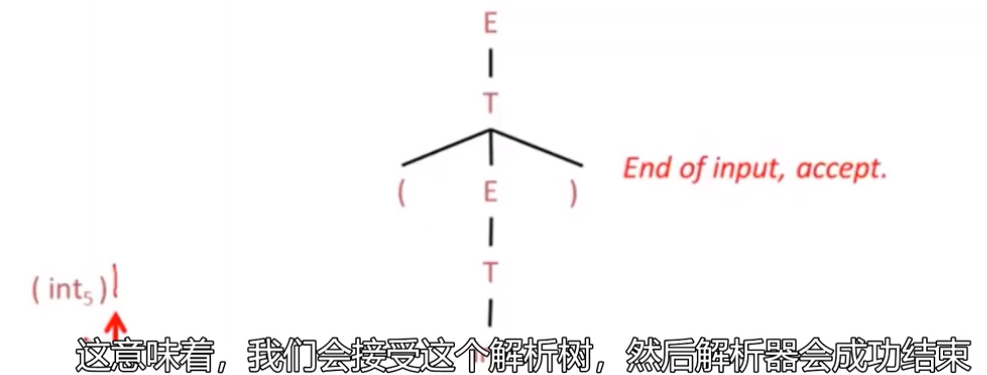
image-20200709093210746

递归下降算法

  • Let TOKEN be the type of tokens
    • Special tokens INT, OPEN, CLOSE, PLUS, TIMES
  • Let the global next point to the next input token

image-20200709093644246

image-20200709100234043

image-20200709100315068

image-20200709100353599

递归下降的局限性

link

  • if a production for non-terminal X suceeds
    • canno backtrack to try a different production for X later
  • General recurisive-descent algorithms support such “full” backtracking
    • Can implement any grammar

递归下降解析的主要难点-左递归 left recursion

image-20200709223432931

image-20200709223907932

image-20200709224244931

PA3

https://github.com/mrbelieve128/Stanford-Compilers-PA/tree/master/PA3

预测解析 Predictive Parsers

预测解析和递归下降很像，依然是自上而下，但能从不出错的预测该使用哪一个产生式，并得出正确的解析。

  • 根据输入字符串中出现的内容，来尝试得出该使用哪个产生式。只适合语法形式很固定的情况
  • 不需要回滚操作。解析器可以完全肯定要使用的产生式

接受 LL(K) 语法 (left-to-right 从左到右 left-most derivate 始终基于解析树上最左非终结符 k tokens lookahead)

如

image-20200721124025300

实际上是使用表格记录数据

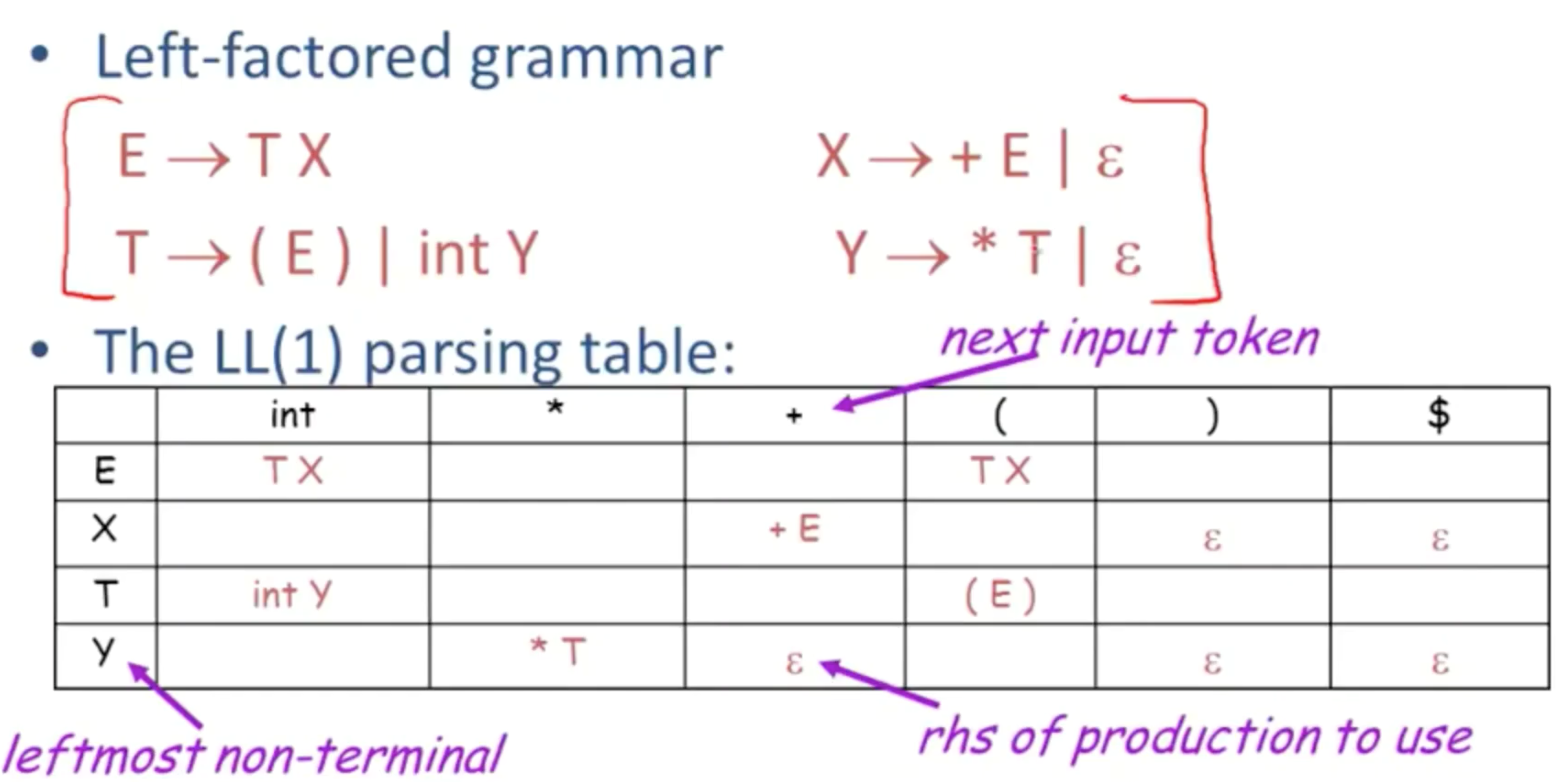
image-20200721124104017

使用栈记录边界

  • 把最左终结符或非终结符始终放在栈顶

算法

image-20200721201621877

  • 使用S和$初始化栈。
  • $标记栈底，可以看作输入结束的标记。
  • 如果栈顶是最左非终结符，根据解析表来查找非终结符为X和下一个输入字符所对应的产生式右手边内容，然后弹出栈顶的X。如果不符合就会报错，因为没有回滚操作，没有办法解析字符串。
  • 如果栈顶是终结符的话，试着匹配输入，匹配成功就移动到下一个输入元素，然后弹出栈顶元素。如果不符合就会报错，因为没有回滚操作，没有办法解析字符串。

image-20200721201531558

First集 First Sets

构建LL(1) 解析表

non-terminal A, input singal t

什么时候T[A,t] = α（意思是解析表上[A, T]这一单元格里的内容是α

image-20200722154608118

image-20200722160201765

例子

左边是terminal的first集，只包含自身，右边是non-terminal的

image-20200722160742081

Follow集 Follow Sets

Follow集中的元素是那些被用到的元素而不是生成的符号。ε不会加进Follow集中

image-20200722162012683

image-20200722162135668

一些规则

出现在产生式右侧末尾的，如E -> TX Follow(E) 是Follow(X)的子集

image-20200722164420950

而在E -> TX 中，X可以消除，所以Follow(E) 同样是Follow(T)中的元素

’ ( ‘的Follow集就是First(E)中所有元素，而First(E) = First(T)

Follow(’+’) = First(E)

Follow(int)因为可以Y可以变成ε，所以Follow(T)中的元素也会是Follow(int)中的元素

image-20200722165632093

LL(1)解析表

目标是为上下文无关语法G构建出一个解析表T

语法/规则

image-20200722223652295

例子

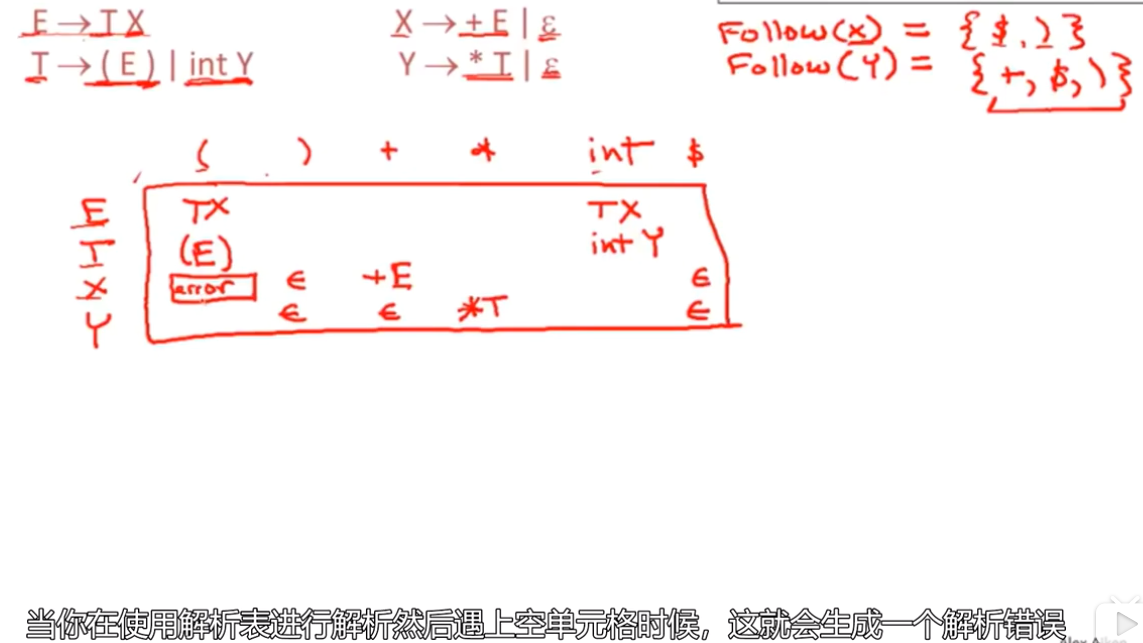
image-20200722224646095

根据字母（非终结符）和符号（终结符）来预测和匹配完整的对应关系

构建完解析表的时候，如果表格内的某些单元格中有多种操作的话，每种情况下的操作就不是唯一的，这就不是LL(1)语法。

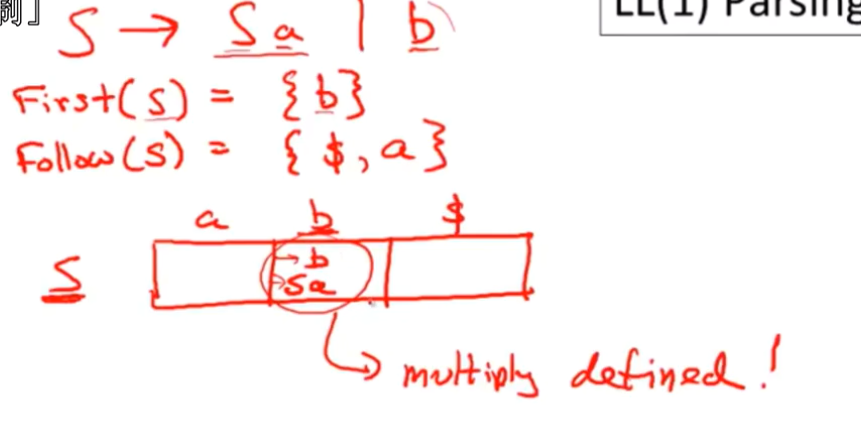
image-20200722225221200

自下而上的解析 Bottom-Up Parsing

Bottom-Up 解析比top-down 递归下降解析 更通用，且同样高效

Bottom-Up是大部分解析生成工具所使用的一种首选方法

  • 不需要提取左因子语法
  • 回归到“正常”语法，但仍然需要对**+号和号*的优先权进行编码
  • 不会处理语义混淆的语法

Bottom-Up解析 会进行归约，既通过反转产生式，逆向替换，将字符串规约为起始符号

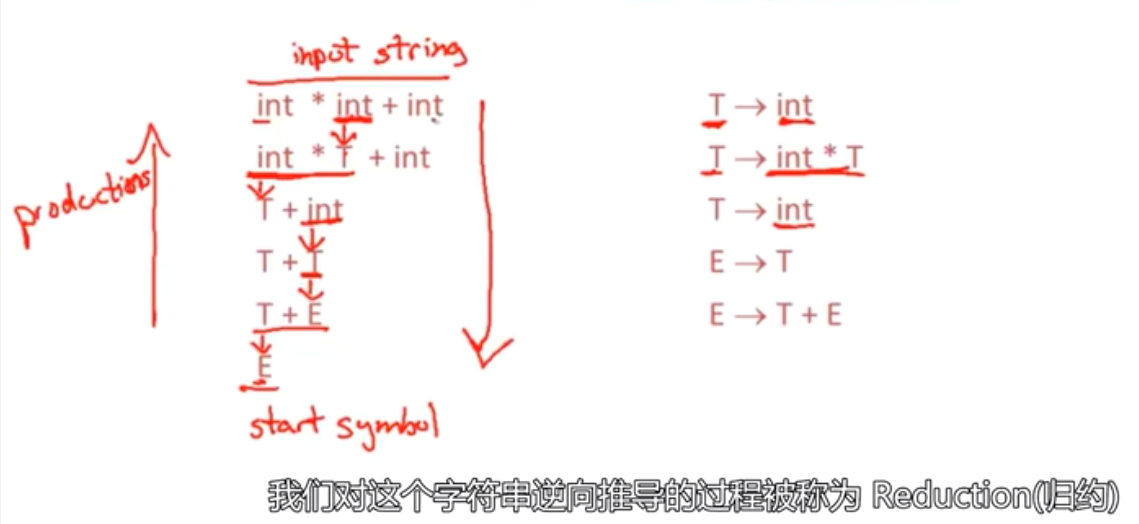
image-20200723094219185

从下往上看，是最右推导

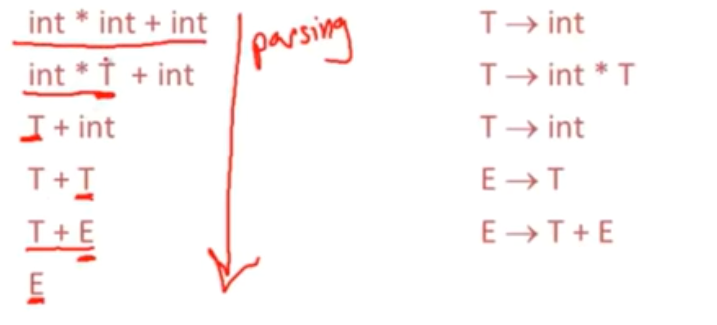
image-20200723094508872

解析树，也是从下往上生成的

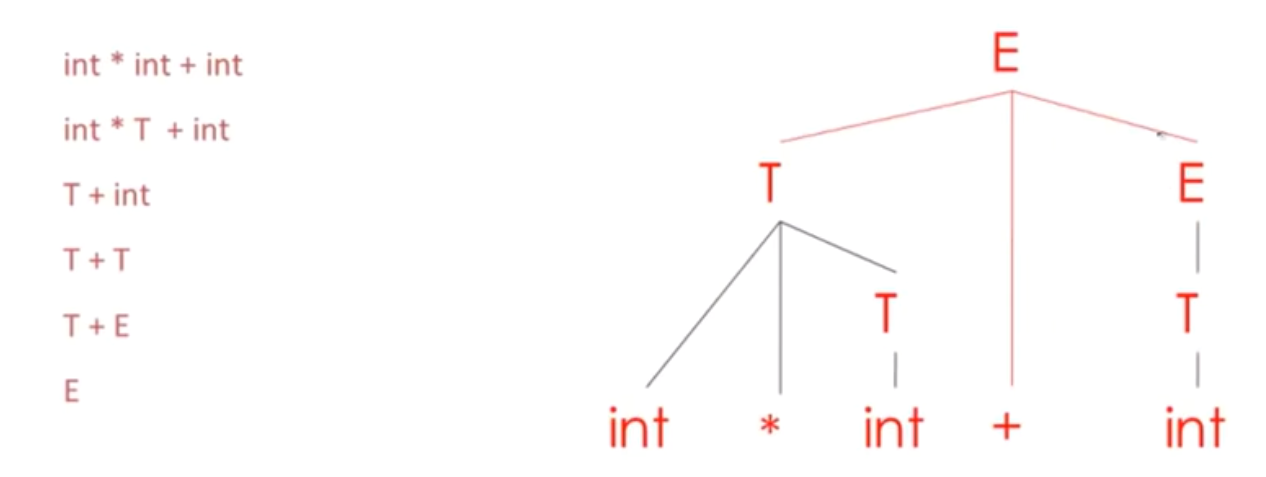
image-20200723094848086

移位规约解析 Shift Reduce Parsing

image-20200723095155240

在执行规约操作前，始终得需要得到足够多的输入（移位足够多次）

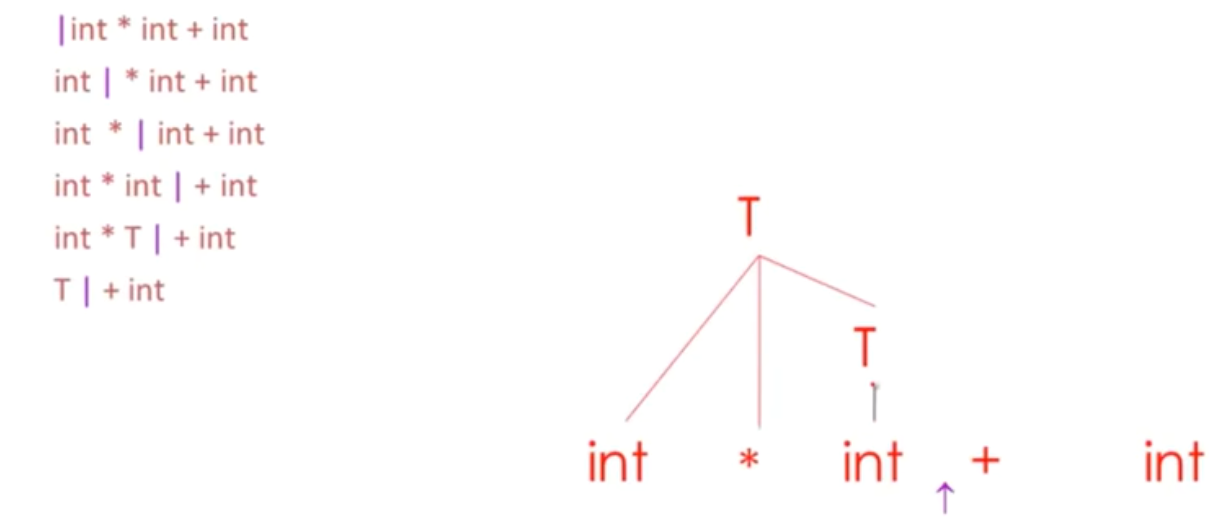
image-20200723095718573

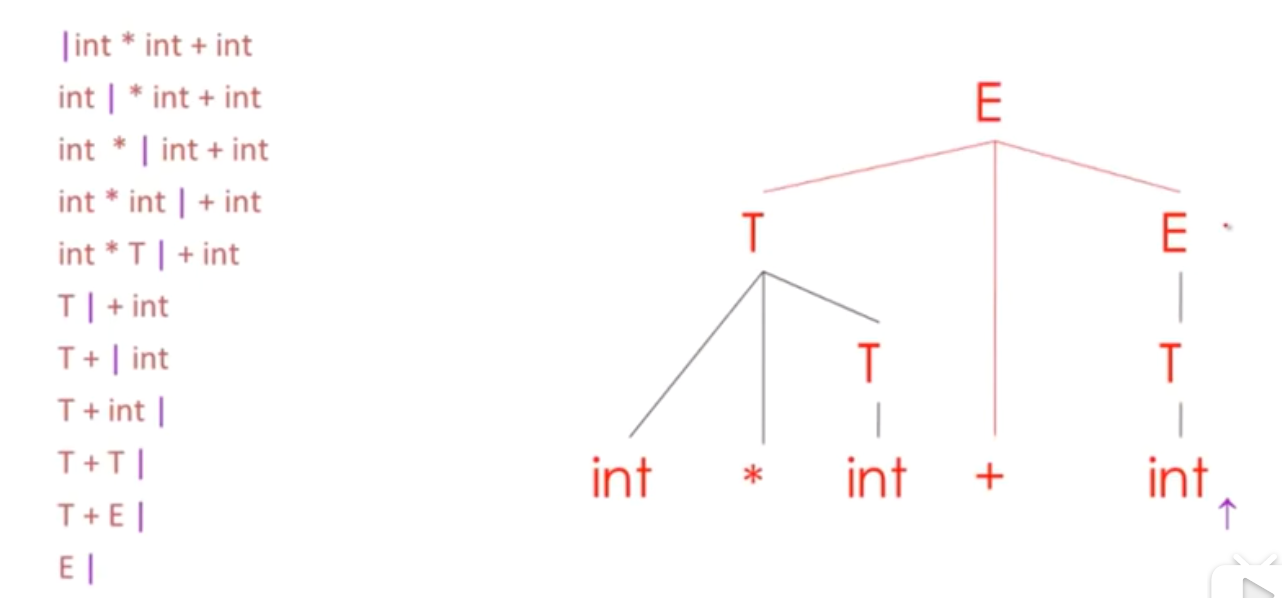
image-20200723095745689

  • 竖线左边的字符串能够由一个栈实现，栈顶就是那个竖线的位置
  • Shift移位操作会push一个terminal进入栈
  • 规约操作，将一些符号弹出栈，这些是产生式右手边的内容。接着会把一个非终结符压入栈中，这歌非终结符是产生式左手边的内容

image-20200723100832481

句柄 Handles

句柄就是一个规约点，可以允许解析器通过进一步的规约操作回到开始符号位置。（句柄就是包含了一个可规约的操作路径）

在shift-reduce解析中，句柄只会出现在栈顶

image-20200723102541174

句柄识别

L代表从左到右扫描，R代表最右推导，K代表了需要向前看k个数量的token

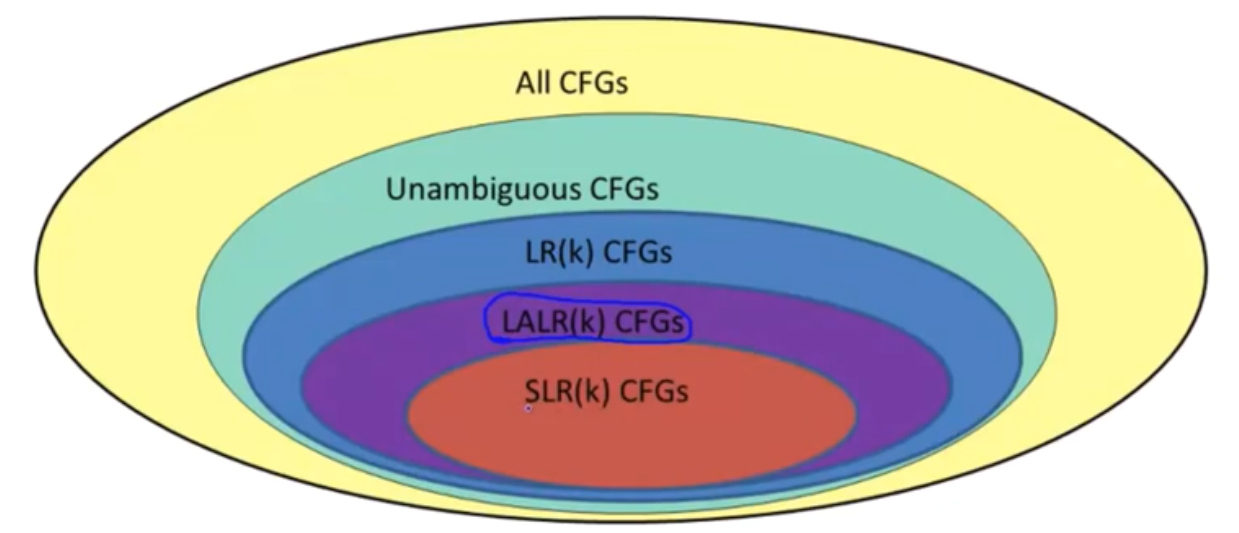
image-20200723103946950

image-20200723104156569

image-20200723104447205

对于任何语法来说，可行前缀集就是一个正则语言

item是指一个产生式右手边某处存在的一个’ . ‘，如 T -> (E) 的item包含 T -> .(E) T -> (.E) T -> (E.) T -> (E).

而 X -> ε 的item是 X -> .

image-20200723105616024

image-20200723105856274

’ . ‘左侧的内容是见过的，即栈内元素。右侧元素则是在进行规约操作前想要读取的内容。

image-20200723111109950

image-20200723112430462

从底向上开始处理

image-20200723112639904

识别可行前缀 Recognizing Viable Prefixes

目标是去写一个非确定性有限自动机来识别解析器中有效的栈

image-20200723152951096

感觉是推算所有的可能性

有效item Valid items

The states of the DFA are “canonical collections of items” or “canonical collections of LR(0) items”

定义

image-20200723155218728

简化地说

image-20200723155456565

image-20200723155514814

语义分析 Semantic Analysis

语义分析简介

为什么需要单独一个语义分析阶段？

  • 编程语言会有一些特征，人可能会犯一些解析无法捕获的错误
  • 一些语言结构并非上下文无关

语义分析实际上做什么

如coolc的检查列表

  1. 所有标识符被声明，作用域是否规范
  2. 类型检查（主要功能）
  3. 继承关系是否有意义
  4. 类仅定义一次
  5. 类中方法也只被定义一次
  6. 不滥用保留的关键字标识符
  7. ……

Scope

目标: 将用法和声明相匹配

静态分析在大多数语言中都相当重要

image-20200723162419518

image-20200723165607420

在下面例子中，对于X可能会有歧义，则使用最近嵌套规则 most closely nested rule

image-20200723170146809

image-20200723170623797

Symbol Tables

在许多编译器中的一种重要的数据结构

image-20200723171535802

image-20200724094925936

image-20200724095151576

会先找最近的Y（也就是最新定义的）

而在下述错误示范中，为了解决这个问题

f(x:INT, x:INT)
{}

image-20200724095821453

check_scope直到x处在栈顶才返回true

因为cool中可以，class名先用再定义，所以不可能通过symbol table或在一次检查中检查完class名

解决办法

  • 第一次检查：记录所有的class名
  • 第二次检查：检测

语义分析通常要求多次检查，而且经常大于两次检查。

Types

image-20200724102140619

一种语言的type system定义了哪些类型能使用哪些操作符，目标是操作符只被正确的类型使用

目前，有三种类型语言：

  • 静态类型：编译的时候就检测类型
  • 动态类型：直到执行代码才检测类型
  • untyped：没有类型检测（机器代码 ）

静态类型喝动态类型的看法

image-20200724103636901

Type Checking image-20200724105958685

image-20200724110021635

image-20200724110937602

Type Environments

image-20200724111334320

image-20200724111354123

image-20200724111528046

image-20200724111731184

image-20200724112015350

image-20200724112448369

image-20200724112420945

image-20200724112952700

image-20200724113344525

Subtyping

image-20200724141347149

image-20200724141650601

image-20200724142110637

LUB or least upper bound

image-20200724142626399

image-20200724143528841

image-20200724143822176

因为不知道会匹配上哪个类型，所以要lub(T1,…..Tn)

Typing Methods

image-20200724144324764

image-20200724144914464

image-20200724145112483

image-20200724145555997

image-20200724145757350

image-20200724150056109

image-20200724150109672

Implementing Type Checking

image-20200724151522565

image-20200724151938870

image-20200724152341217

PA4

Cool Type Checking & Runtime Organization

Static vs. Dynamic Typing

Static type systems detect common errors( at compile time)

But some correct programs are disallowed

  • Some argue for dynamic type checking instead
  • Others want more expressive static type checking

Soundness theorem: for all expressions E

dynamic_type(E)=static_type(E)

In all executions,E evaluates to values of the type inferred by the compiler.

image-20200803110654648

Self Type

class Count{
 i:int-0; 
 inc():Count{//返回Count的class类型
  {
   i<-i+1; 
   self;
  }
 };
};

class Stock inherits Count{
 name: String;--name of item
}
class Main{
 Stocka-(new Stock).inc();//类型错误，Count不是Stock的子集
 ...a.name ...
}

image-20200803112048486

Self Type Operations

image-20200803112942180

image-20200803113101122

image-20200803113408665

image-20200803114939592

image-20200803115337069

Self Type Usage

image-20200804090907495

image-20200804090921258

image-20200804091404056

Self Type Checking

image-20200804094143731

image-20200804094222838

image-20200804094434305

image-20200804094508391

image-20200804094930978

image-20200804094952794

Error Recovery

image-20200804100054994

image-20200804095353003

a workable solution but with cascading errors

image-20200804100442013

image-20200804100525228

Runtime Organization

Enforcing the language definition is just one purpose of the front-end. The front-end also builds the data structures that are needed to do co-generation as we seen but there is a real. Once we get through the front-end we no longer looking for errors in the program. We’re no longer trying to figure out whether it’s a valid program. Now we’re really down to the point where we’re going to generate code And that is a job at the back end.

image-20200804100935737

image-20200804101607087

Activations

Two goals:

  • Correctness
  • Speed

Complications in code generation come from trying to be fast as well as correct

image-20200804102036374

image-20200804103800174

image-20200804103904151

activation tree

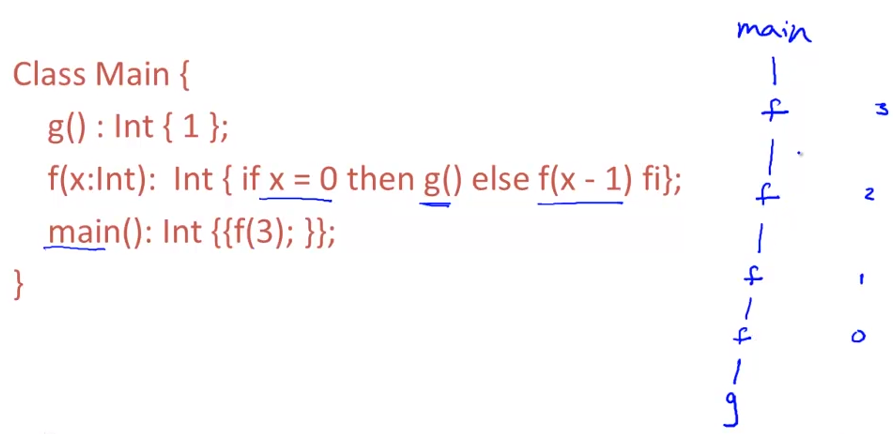
image-20200804104501937

子树在同一行内代表调用后，需要依次调用的函数

isEven(x:Int) : Bool {x % 2 == 0};
isOne(x:Int) : Bool {x == 1};
powerOfTwo(x:Int) : Bool {
if isEven(x) then powerOfTwo(x / 2)
else isOne(x)
};

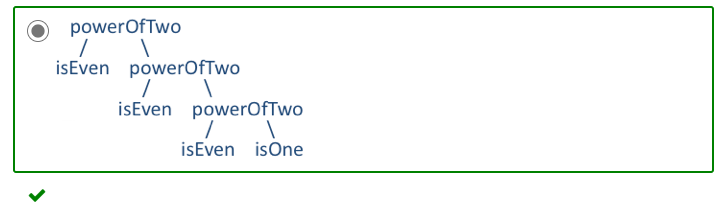
image-20200804105015043

Activation Records

The information needed to manage one procedure activation is called an activation record (AR) or frame

If procedure F calls G, then G’s activation record contains a mix of info about F and G.

image-20200804105747132

The compiler must determine,at compile-time,the layout of activation records and generate code that correctly accesses locations in the activation record

Thus,the AR layout and the code generator must be designed together!

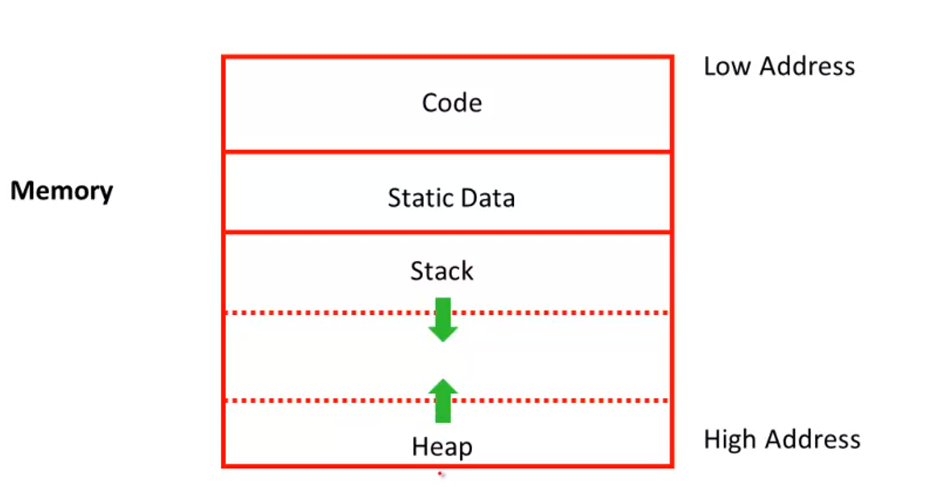
Globals and Heap

image-20200804111927233

Both the heap and the stack grow

Must take care that they don’t grow into each other

Solution:start heap and stack at opposite ends of memory and let them grow towards each other

image-20200804112106101

Alignment

image-20200804112719766

Stack Machines

image-20200804112851657

image-20200804113208145

image-20200804113359758

image-20200804114035608

image-20200804114216478

After evaluating an expression e, the accumulator holds the value of e and the stack is unchanged.

Expression evaluation preserves the stack.

exmaple

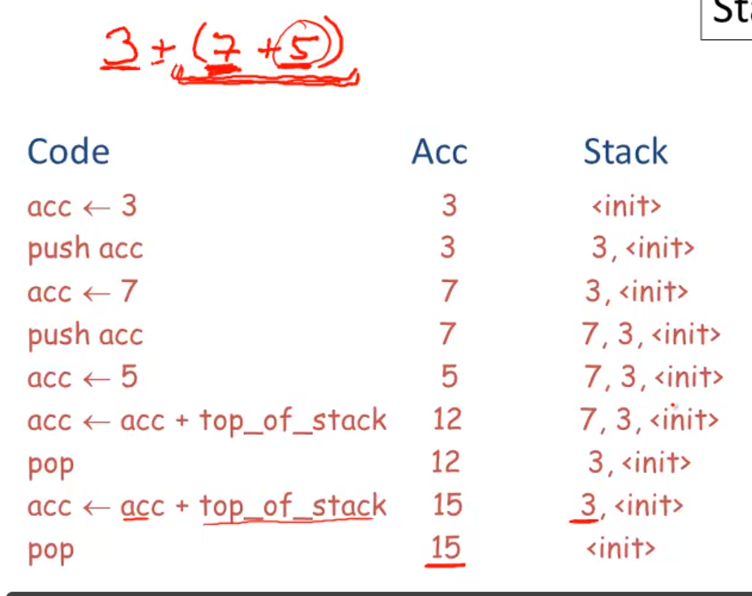
image-20200804115009773

Code Generation

Introduction to Code Generation

The accumulator is kept in MIPS register $a0

The stack is kept in memory

  • The stack grows towards lower addresses
  • Standard convention on MIPS

The address of the next location on the stack is kept in MIPS register $sp (stack pointer

  • The top of the stack is at address $sp+4

Stack is growing towards low addresses

image-20200808090532307

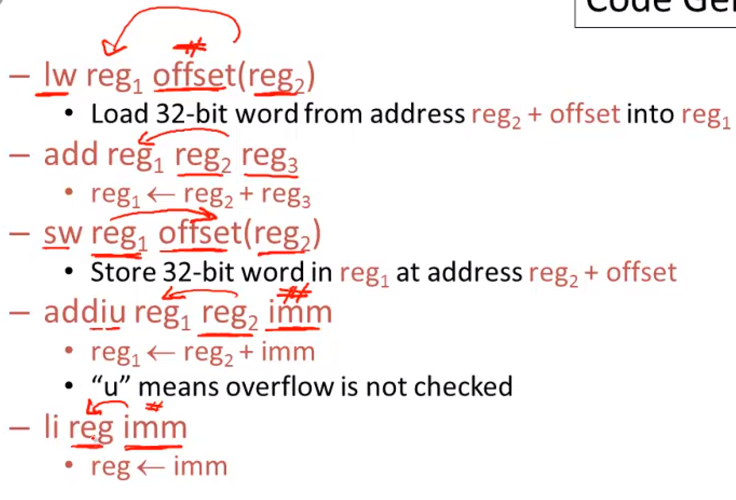
image-20200808090733566

example

image-20200808090948399

Code Generation I

image-20200808092449719

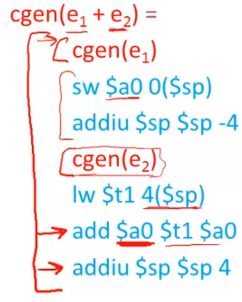
image-20200808092520377

image-20200808092406241

image-20200808092138761

image-20200808092837102

image-20200808093434286

Code Generation II

image-20200808101554898

image-20200808101652847

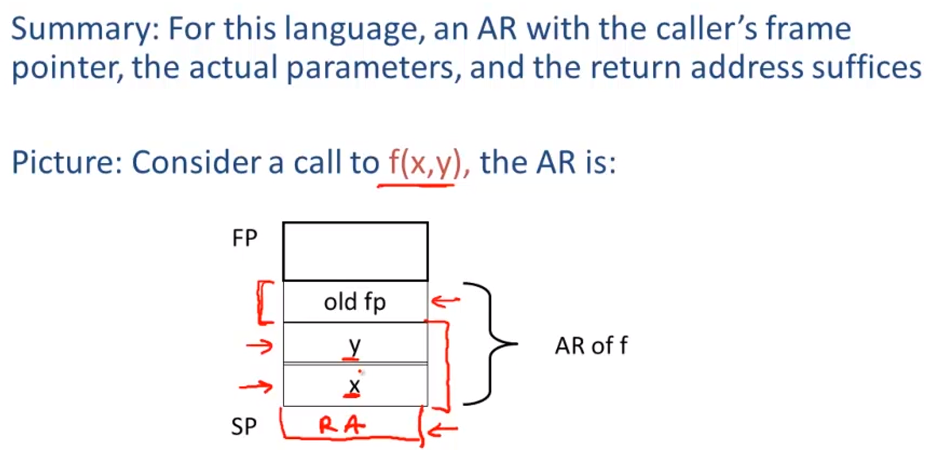
image-20200808101826630

image-20200808102115320

image-20200808102420307

image-20200808102625336

image-20200808102731121

example

image-20200808103106476

image-20200808103516812

image-20200808103618842

Code Generation Example

image-20200808104801419

Temporaries

Idea:Keep temporaries in the AR

The code generator must assign a fixed location in the AR for each temporary

image-20200808113002505

While we need one here for the predicate, but notice that once the predicate is decided, once we know the answer to whether this predicate is true or false, we don’t need that temporary anymore. So in fact, that temporary can be reclaimed; we don’t need the space for that temporary anymore by the time we get to the false branch.

image-20200808112920088

NT(e1 + e2) = max(NT(e1), 1 + NT(e2))

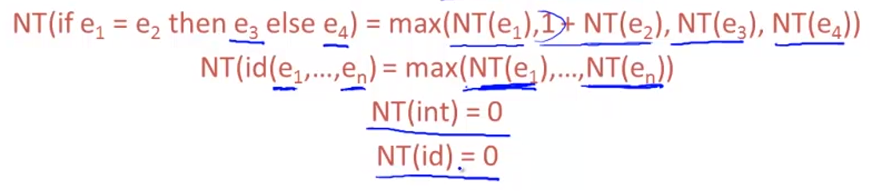
image-20200808113708280

example

image-20200808113903169

最多需要两个temporaries来储存这些数据

if 的true 或flase 一个，单个int可以变成返回值（不用临时变量），调用fib 传递的参数需要用临时变量

For a function definition f(x.…… Xn)=e the AR has 2+n+NT(e) elements

  • Return addressL
  • Frame pointer C
  • n arguments
  • NT(e) locations for intermediate results

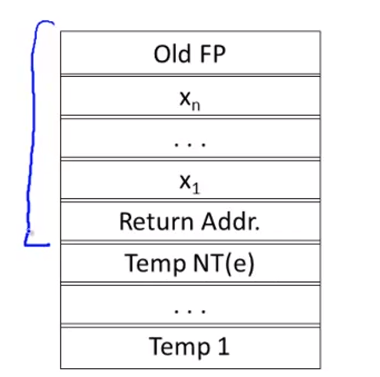
image-20200808114653932

new scheme

image-20200808115316923

image-20200808115353156

nt unused temporary

Object Layout

00 implementation=Basic code generation + More stuff

0o Slogan:If B is a subclass of A,than an object of class B can be used wherever an object of class A is expected

This means that code in class A works unmodified for an object of class B

image-20200808120906584

image-20200808121002133

image-20200808121205970

image-20200808120828905

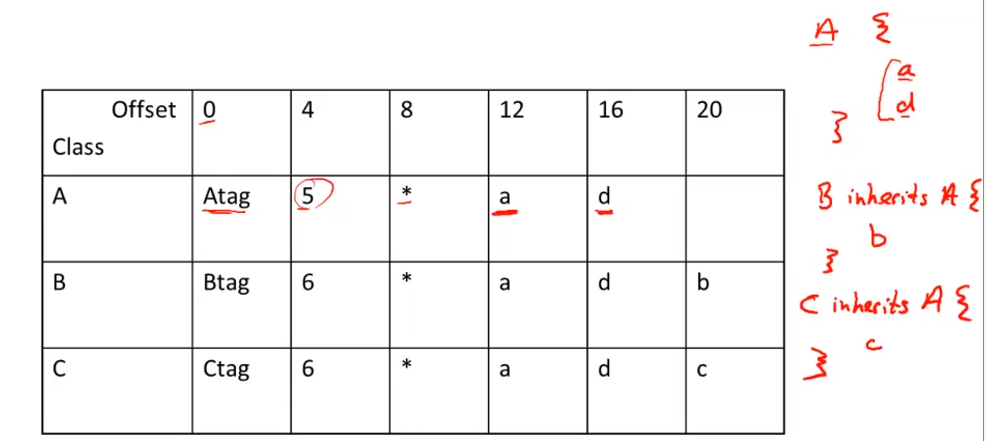
image-20200808120723112

image-20200808121617559

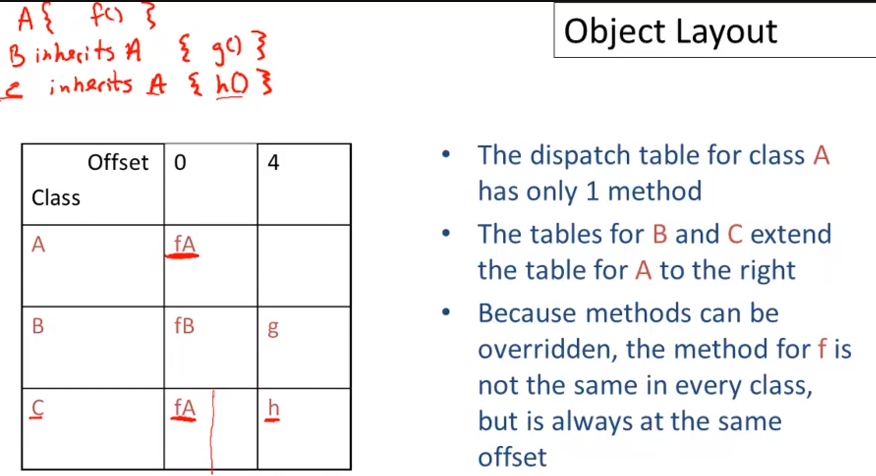
Every class has a fixed set of methods

  • including inherited methods

A dispatch table indexes these methods

  • An array of method entry points
  • A method f lives at a fixed offset in the dispatch table for a class and all of its subclasses

image-20200808122344016

image-20200808122753473

image-20200808122815394

opentional Semantics overview

We must specify for every Cool expression what happens when it is evaluated

  • This is the"meaning"of an expression

The definition of a programming language:

  • The tokens >lexical analysis
  • The grammar >syntactic analysis
  • The typing rules >semantic analysis
  • The evaluation rules →code generation and optimization

image-20200808142452501

image-20200808142730543

Denotaional semantics

Program’s meaning is a mathematical function

Axiomatic semantics

  • Program behavior described via logical formulae
    • If execution begins in state satisfying X,then it ends in state satisfyingY
    • X,Y formulas
  • Foundation of many program verification systems

Operational Semantics

image-20200808143144331

image-20200808143427301

A variable environment maps variables to locations

  • Keeps track of which yariables are in scope
  • Tells us where those variables are

E = [ a : l1, b : l2 ]

image-20200808144113316

image-20200808144211557

image-20200808144502293

image-20200808144825648

Cool Semantics

image-20200808145028046

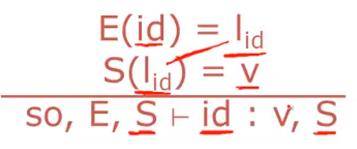
image-20200808145137544

first we look up in the environment E where that identifier id is stored so now we give us back a memory

location l. So by in this case And then we look up in the store S what the value is at that memory locations, So,

we use the same memory location here as an argument to the store to get back the value that variable currently

has And notice I just have a reference, this is a read of memories so this is loading, I think it was loading the

value of the variable. This does not affect the store so the store S is the same before and after. This is just looking

at the value

image-20200808145557313

assignment

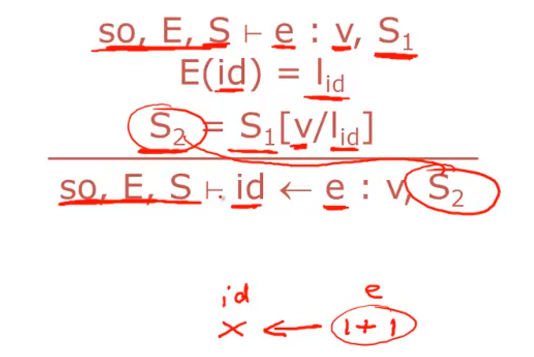
image-20200808145750438

image-20200808145944381

we modify the store at that point with the new value so we replace the location l id or we update the value of l, i, d to be the value of v and we do that in store s1 which gives us a new store s2.

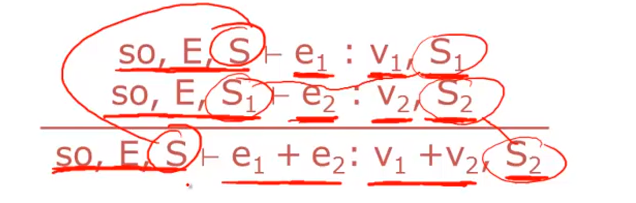
image-20200808150452154

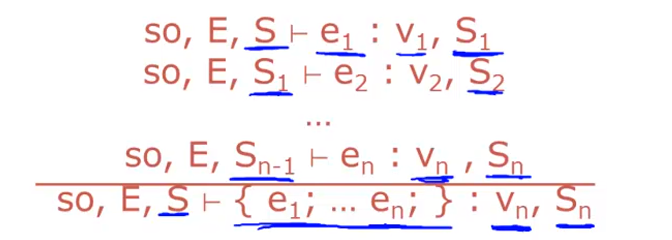
image-20200808150819402

image-20200808151558053

image-20200808151807567

if else

image-20200808151959085

while

image-20200808152117753

image-20200808152158870

let

image-20200808152603765

image-20200808152652618

Cool Semantics II

new

image-20200808153226162

image-20200808153301600

image-20200808153553893

image-20200808154013836

image-20200808154217191

dynamic dispatch

image-20200808154401563

image-20200808154927736

image-20200808155513811

image-20200808155706318

image-20200808155830158

PA5

优化 Optimization

Intermediate Code

image-20200724164441833

image-20200724164545484

image-20200724164657828

image-20200724165004707

Optimization Overview

image-20200727113032723 image-20200727113227764

image-20200727114137055

image-20200727114346148

image-20200727135941770

image-20200727140110611

image-20200727141024199

image-20200727142541805

Local Optimization

有些可以删除的

x = x + 0
x = x * 1

有些可以简化的

x = x * 0 => x =0
y = y ** 2 => y = y * y
x = x *8 => x = x << 3
x = x * 15 => t = x << 4;x = t - x;

（一些机子上«比*号快

image-20200727143956671

image-20200727144813527

保留最高精度的浮点数，让架构决定计算结果

image-20200727145423870

image-20200727145657145

Peephole Optimization

image-20200727150656620

Dataflow Analysis

image-20200727152656236

image-20200727152915293

Constant Propagation

image-20200727153509070

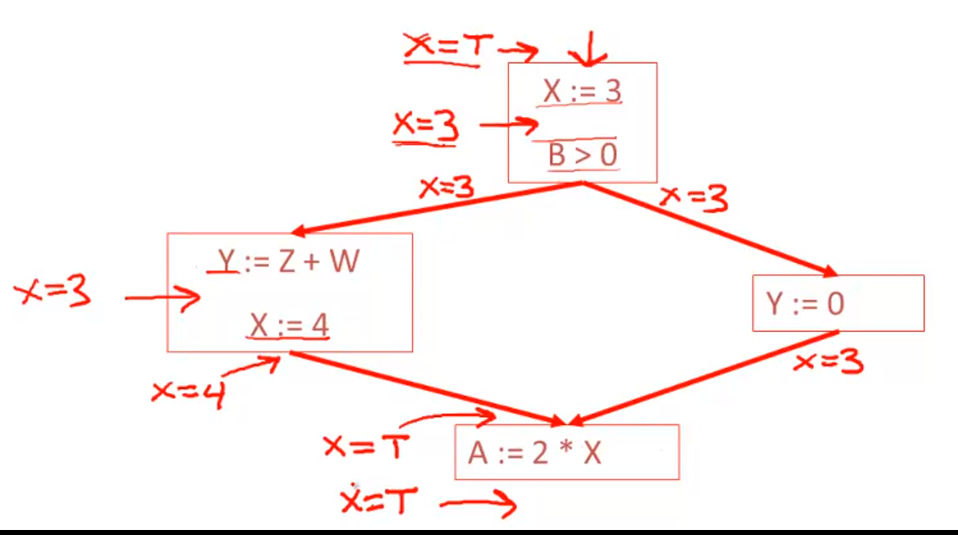
image-20200727154004049

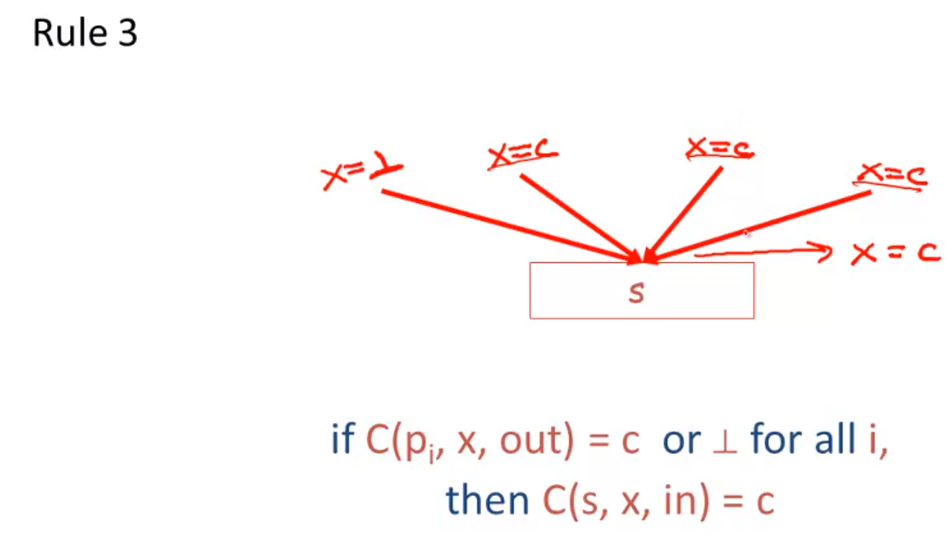
image-20200727154640486

image-20200727155002293

Analysis of Loops

image-20200727161011290

Orderings

image-20200727162943132

image-20200727163013545

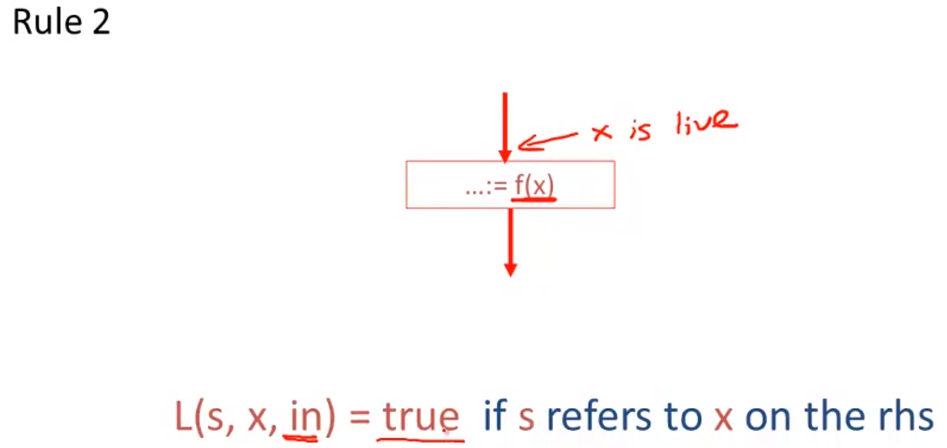
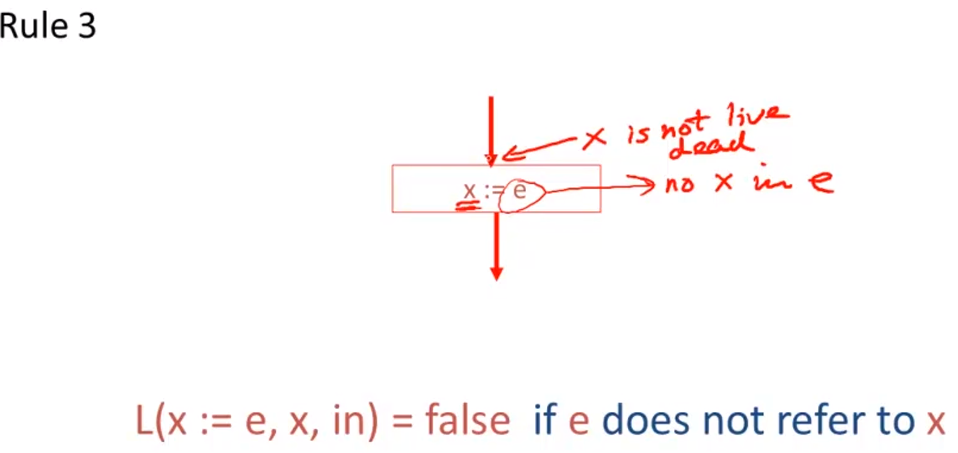
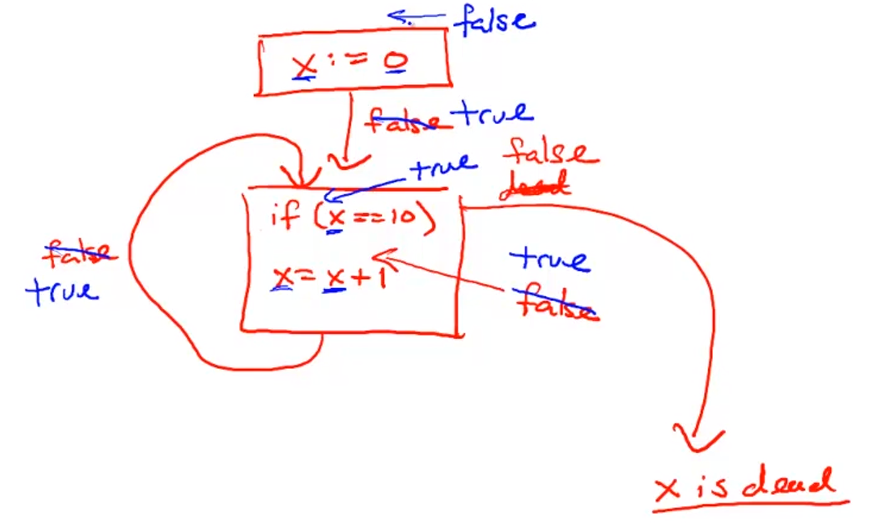
Liveness Analysis

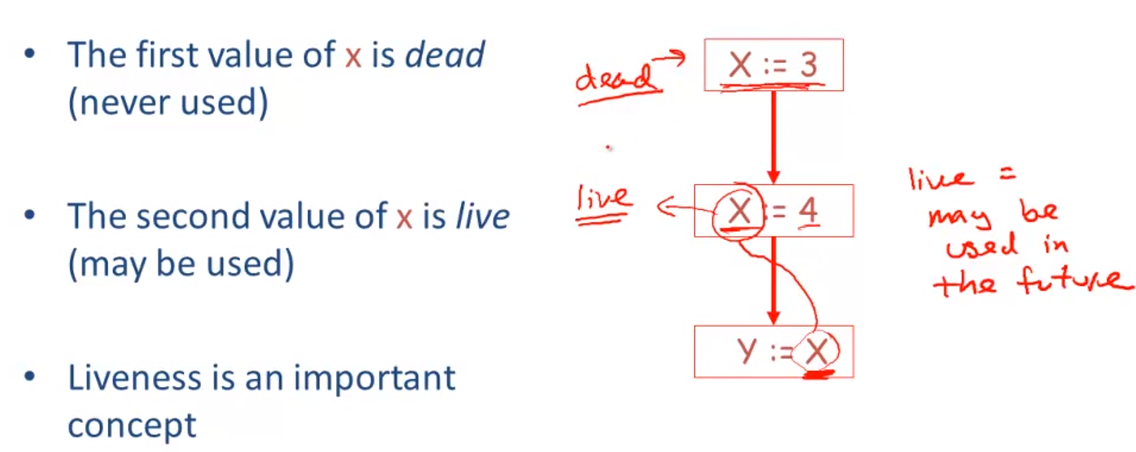
image-20200727164706188

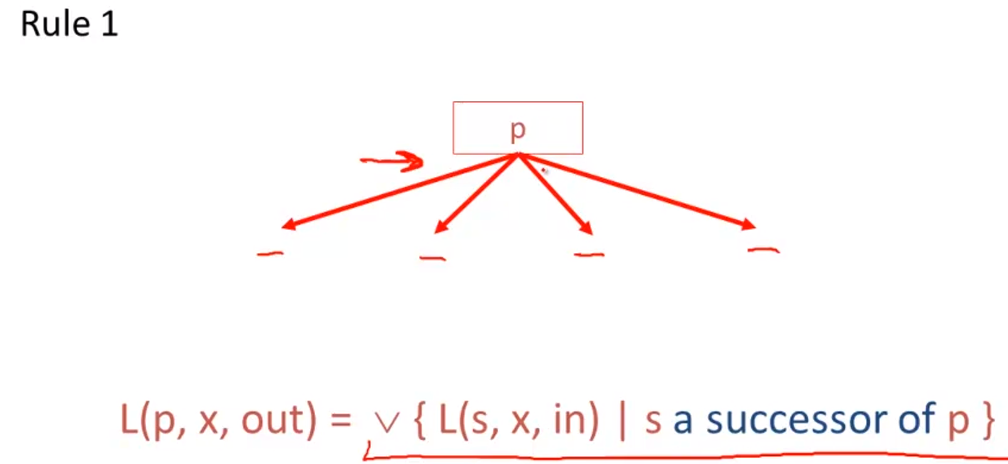
image-20200727164954867

image-20200727165049700

image-20200727165134688

image-20200727165215533

image-20200727165457537

image-20200727165949003

Register Allocation

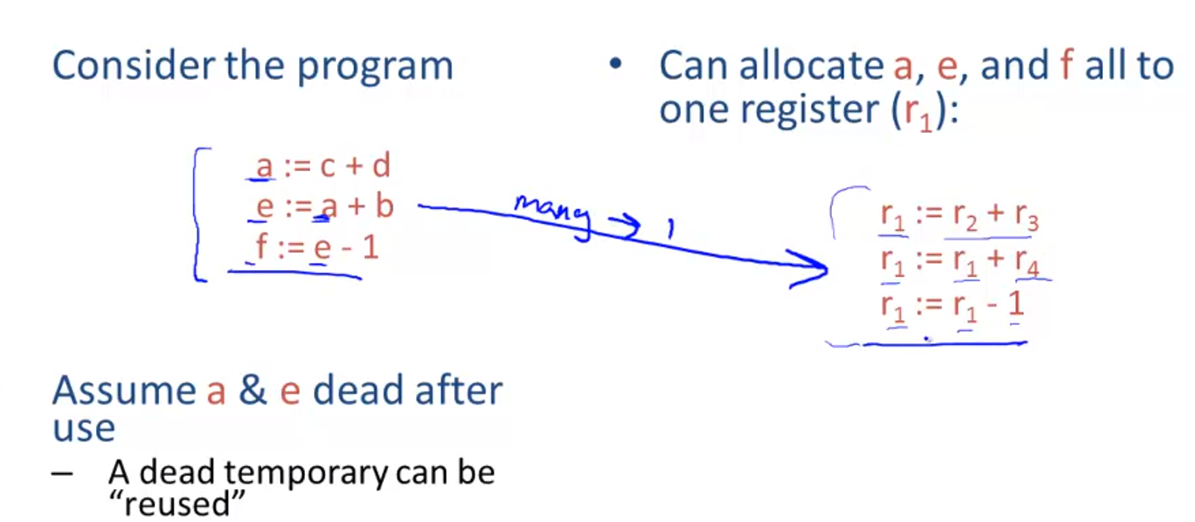
image-20200730092739618

principle

image-20200730093244462

image-20200730093639654

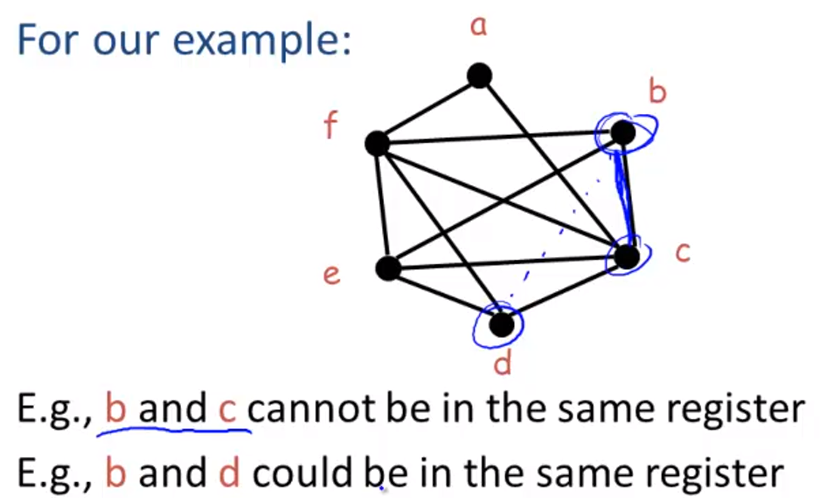
image-20200730093758586

image-20200730094201480

Graph Coloring

A coloring of a graph is an assignment of colors to nodes, sch that nodes connected by an edge have different colors.

A graph is k-colorable if it has a coloring with k colors.In here, colors = registers. Let k = number of machine registers.

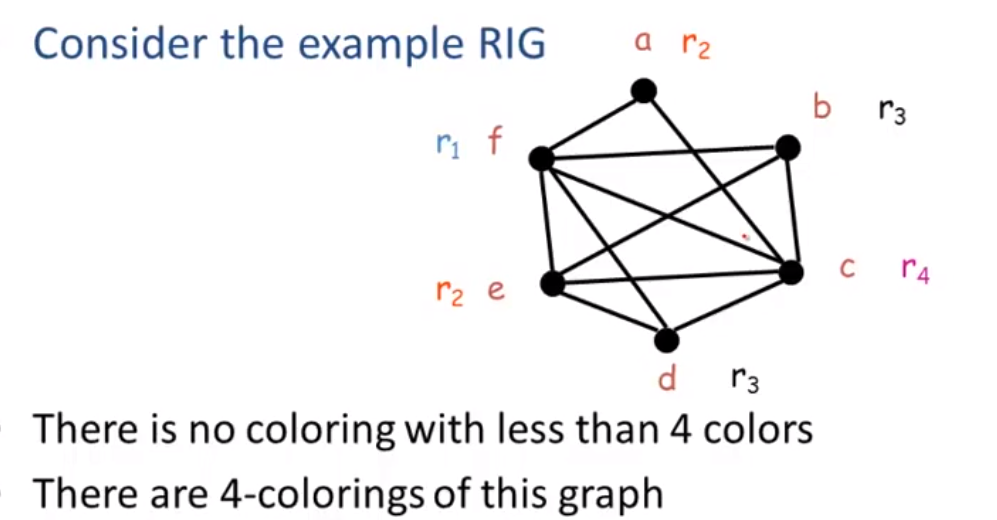
image-20200730100849423

再用寄存器名字替换

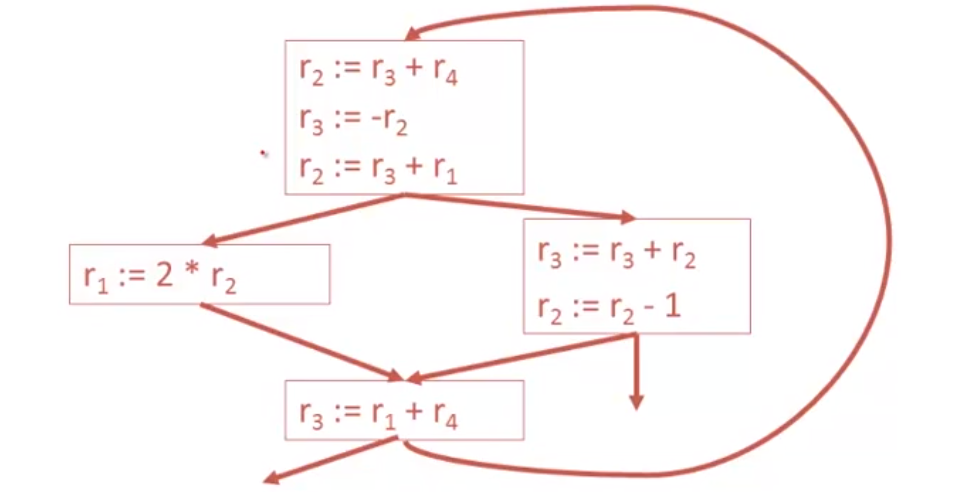
image-20200730101320589

image-20200730104742443

image-20200730105029797

image-20200730105203033

example

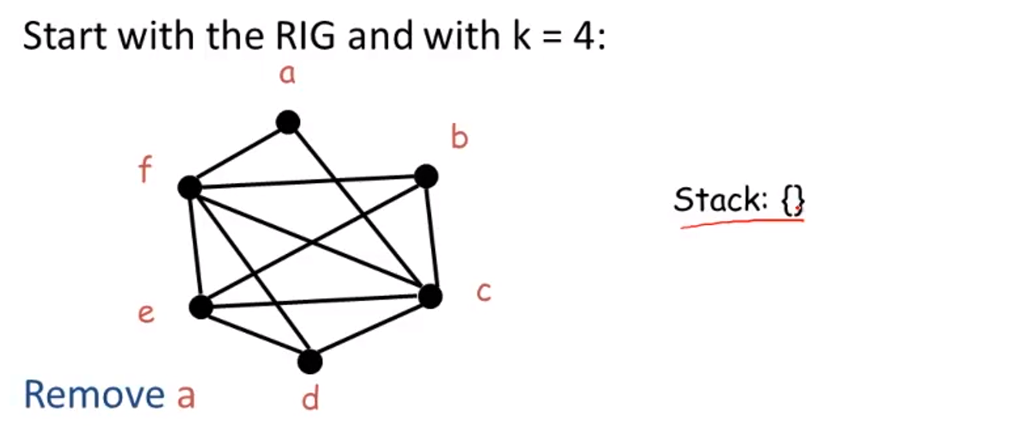
image-20200730105810302

Remove d Stack:{d,a}

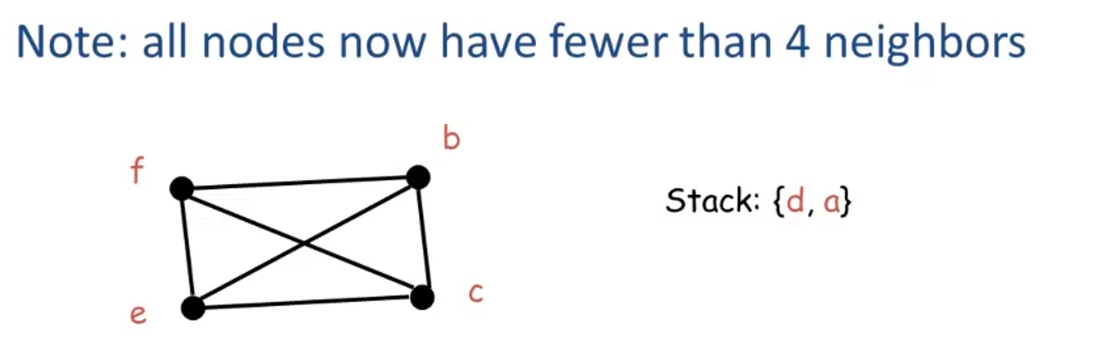
image-20200730105936761

now it doesn’t matter which node we pick because we can process them in any

Remove c,b,e,f

now Empty-graph - done with the first part

image-20200730110258876

going to pick the lowest numbered register that is not used by any of its neighbors.

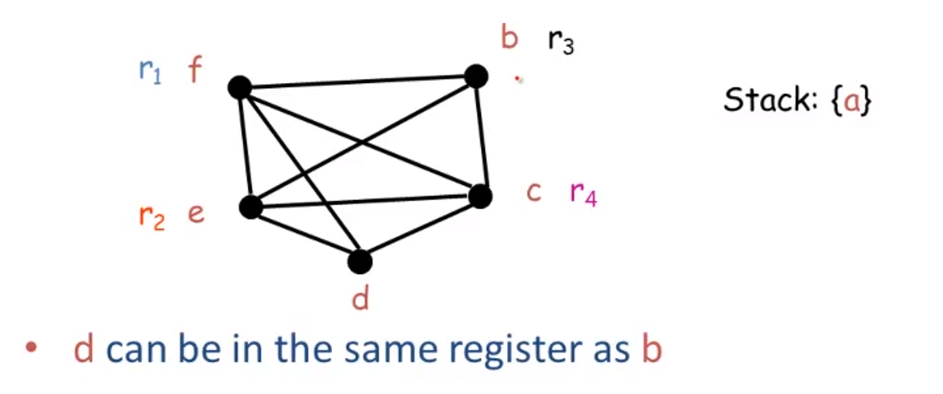
image-20200730110339115

b is the only register that isnt used

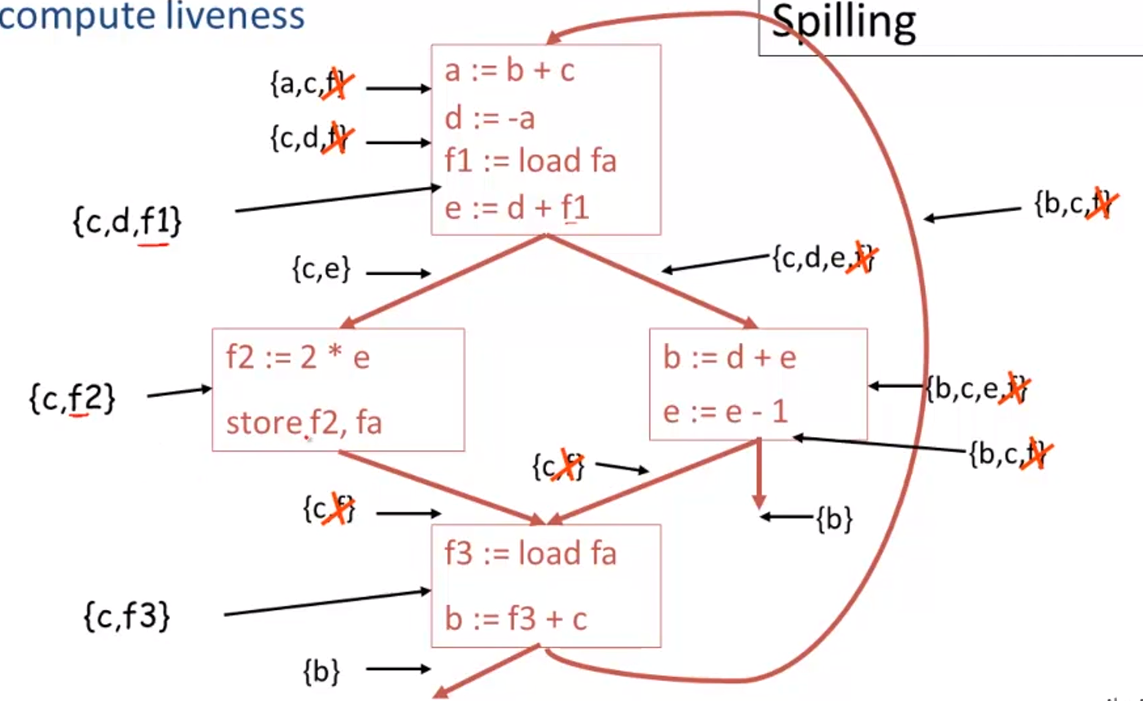
Spilling

if tgere’s no node that we can delete from the graph, in this situation, we’re going to pick and know that there is a candidate for spilling.

  • A spilled value “lives” in memory

optimisitic coloring => hope that among the 4 neighbors of f we use less than 3 colors

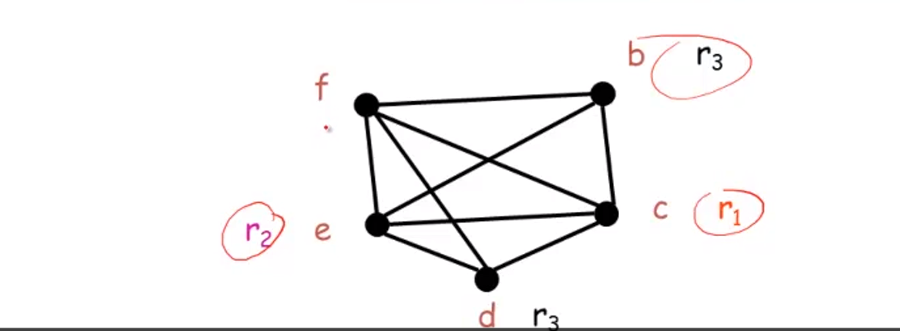
image-20200730112509274

image-20200730112551179

image-20200730113112519

image-20200730112936005

image-20200730113228217

image-20200730113618452

Managing Caches

image-20200730114154225

image-20200730114748858

image-20200730114725025

Garbage collection

Automatic Memory Management

image-20200730144340907

How to know an object will “never be used again”?

image-20200730145148008

image-20200730145452186

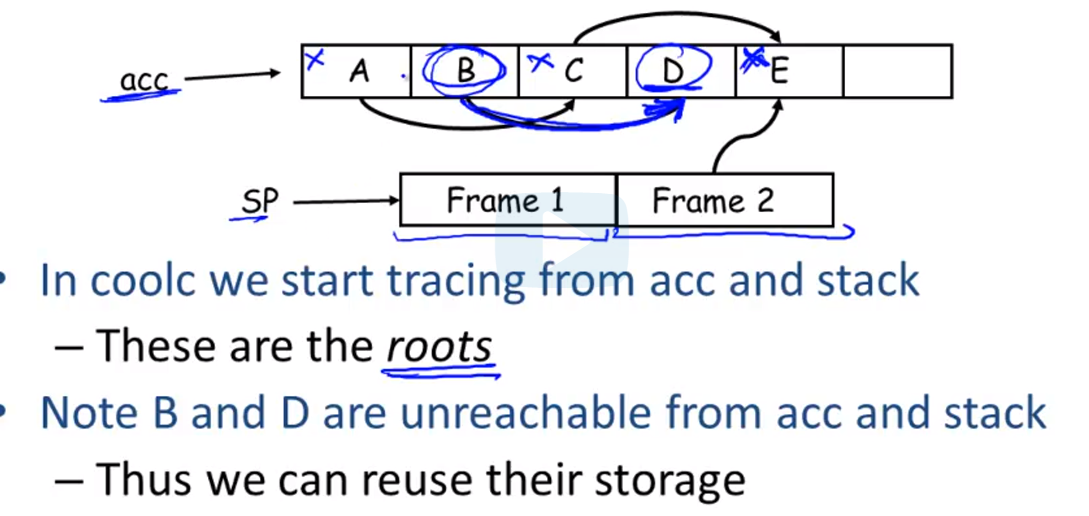
image-20200730150153526

image-20200730150244426

Mark and Sweep

image-20200730150356190

image-20200730150542396

image-20200730162740553

image-20200730163335635

Stop and Copy

当旧区域满的时候，将有用的复制到新区域，然后新旧区域名字对换。

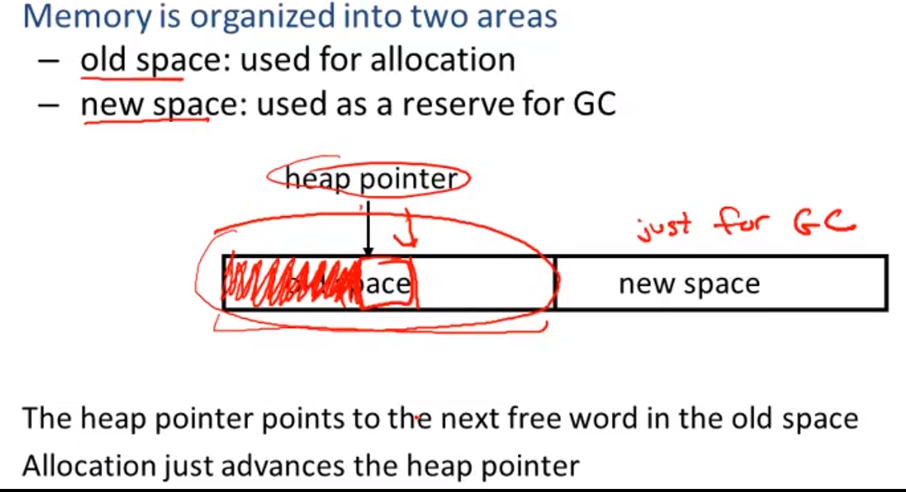
image-20200730171624649

image-20200730171725223

image-20200730172133916

被复制过去之后，指针访问旧区域的时候，会发现旧区域已被标记，然后会更新指针指向新区域

image-20200730172842124

scan到alloc之间就是需要被更新的

solution

先复制A，然后根据指向按序复制到新区域并更新pointer

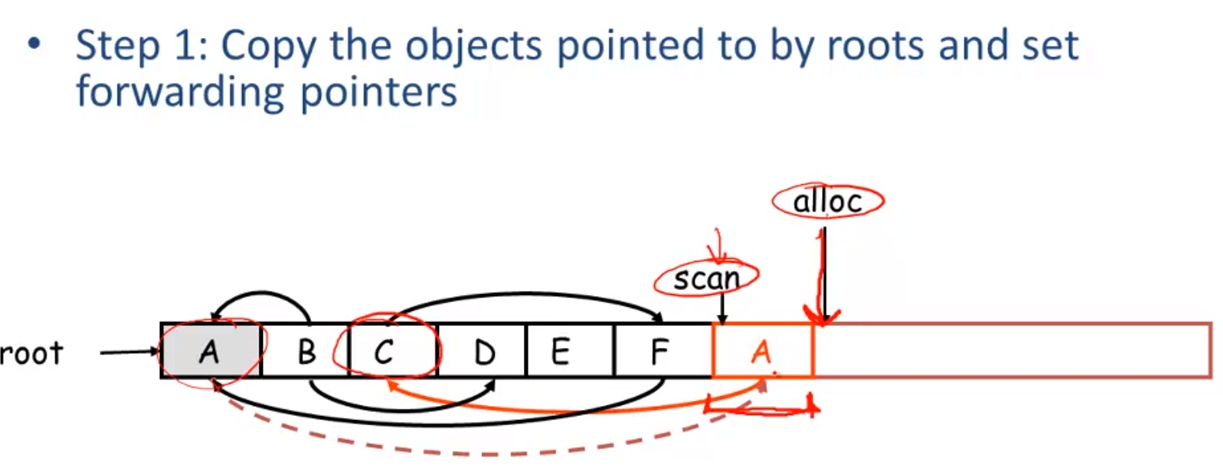
image-20200730173025615

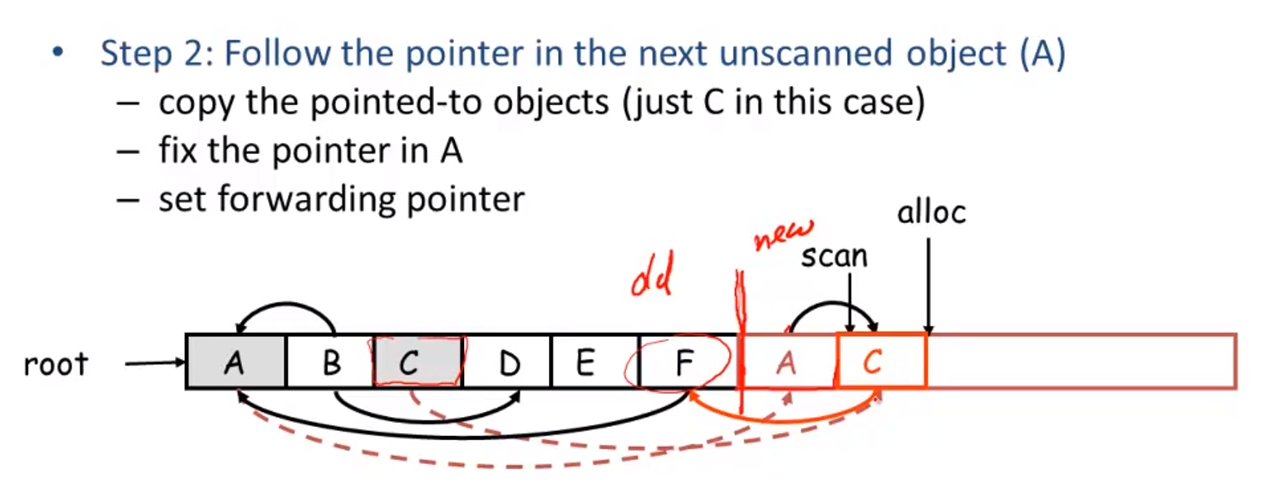
image-20200730173211485

image-20200730174134335

image-20200730174236562

Conservative Collection

image-20200730175043466

image-20200730175410736

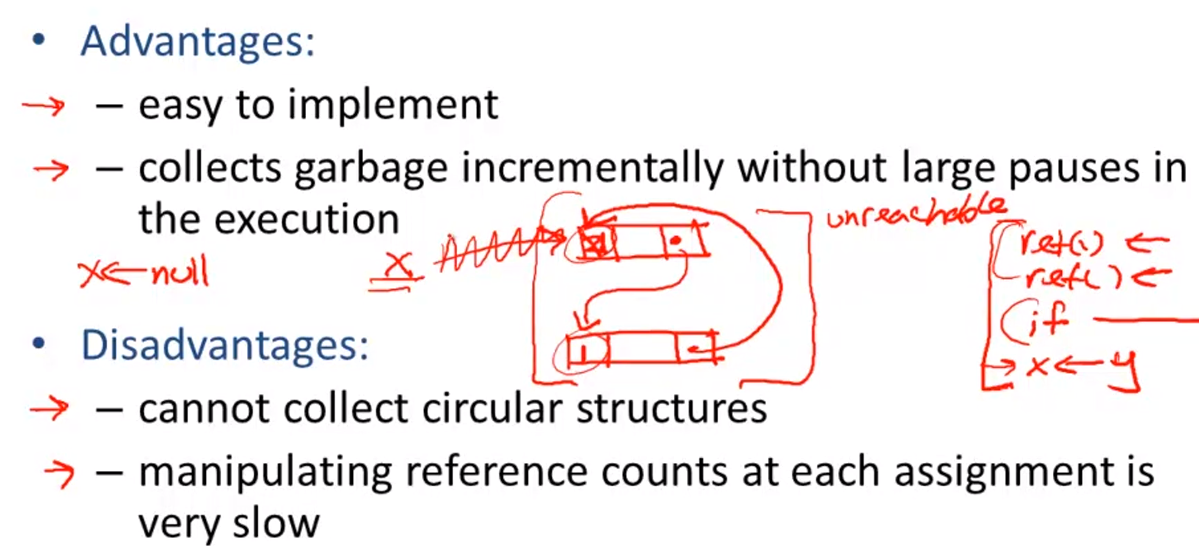
Reference Counting

Try to collect an object when there are no more pointers to it.

image-20200730180530542

image-20200730181146802

image-20200730181841627

image-20200730182213114

「真诚赞赏，手留余香」

Mr.Be1ieVe's Treasure

真诚赞赏，手留余香

使用微信扫描二维码完成支付

CATALOG
    FEATURED TAGS
    awd buu ctf hackthebox linux使用 xray 专业学习 基础知识 学习笔记